
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )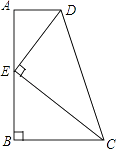
A.CE= ![]() DE
DE
B.CE= ![]() DE
DE
C.CE=3DE
D.CE=2DE
【答案】B
【解析】解:过点D作DH⊥BC,
∵AD=1,BC=2,
∴CH=1,
DH=AB= ![]() =
= ![]() =2
=2 ![]() ,
,
∵AD∥BC,∠ABC=90°,
∴∠A=90°,
∵DE⊥CE,
∴∠AED+∠BEC=90°,
∵∠AED+∠ADE=90°,
∴∠ADE=∠BEC,
∴△ADE∽△BEC,
∴ ![]() ,
,
设BE=x,则AE=2 ![]() ,
,
即 ![]() ,
,
解得x= ![]() ,
,
∴ ![]() ,
,
∴CE= ![]() DE,
DE,
故选B.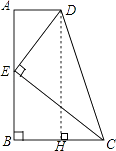
过点D作DH⊥BC,利用勾股定理可得AB的长,利用相似三角形的判定定理可得△ADE∽△BEC,设BE=x,由相似三角形的性质可解得x,易得CE,DE 的关系.本题主要考查了相似三角形的性质及判定,构建直角三角形,利用方程思想是解答此题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】历史上的数学巨人欧拉最先把关于![]() 的多项式用记号
的多项式用记号![]() 的形式来表示(
的形式来表示(![]() 可用其它字母,但不同的字母表示不同的多项式),例如
可用其它字母,但不同的字母表示不同的多项式),例如![]() ,把
,把![]() =某数时的多项式的值用
=某数时的多项式的值用![]() 来表示.
来表示.
例如![]() 时多项式
时多项式![]() 的值记为
的值记为![]() ,
,
已知![]() ,
,![]()
(1)求![]() 的值
的值
(2)若![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,E、F分别相交是AB、CD的中点,EF分别交BD、AC于点G、H。求证:OG=OH。
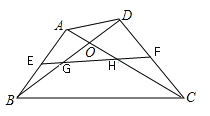
查看答案和解析>>
科目:初中数学 来源: 题型:
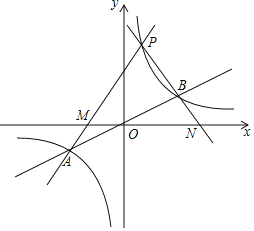
【题目】如图,函数![]() 与
与![]() 图象的交于点A,
图象的交于点A,![]() 若点A的坐标为
若点A的坐标为![]() .
.
![]() 点B的坐标为______;
点B的坐标为______;
![]() 若点P为第一象限内双曲线上不同于点B的任意一点.
若点P为第一象限内双曲线上不同于点B的任意一点.
![]() 设直线PA交x轴于点M,直线PB交x轴于点N,求证
设直线PA交x轴于点M,直线PB交x轴于点N,求证![]() ;
;
![]() 当P的坐标为
当P的坐标为![]() 时,连结PO延长交
时,连结PO延长交![]() 于C,求证四边形PACB为矩形.
于C,求证四边形PACB为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() 、
、![]() ,与x轴相交于C点.
,与x轴相交于C点.
![]() 求点A、B的坐标及直线
求点A、B的坐标及直线![]() 的解析式;
的解析式;
![]() 求
求![]() 的面积;
的面积;
![]() 观察第一象限的图象,直接写出不等式
观察第一象限的图象,直接写出不等式![]() 的解集;
的解集;
![]() 如图
如图![]() ,在x轴上是否存在点P,使得
,在x轴上是否存在点P,使得![]() 的和最小?若存在,请说明理由并求出P点坐标.
的和最小?若存在,请说明理由并求出P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的正三角形ABC中,P0是BC边的中点,一束光线自P0发出射到AC上的点P1后,依次反射到AB、BC上的点P2和P3(反射角等于入射角). 
(1)若∠P2P3B=45°,CP1=;
(2)若 ![]() <BP3<
<BP3< ![]() ,则P1C长的取值范围是 .
,则P1C长的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com