

���� ��1���ɵ���ֱ�������ε����ʵõ�AP=BP=$\frac{\sqrt{2}}{2}$AB=2��������������λ�ߵ����ʣ��õ�EF��AB��EF=$\frac{1}{2}$AB=$\sqrt{2}$�����ɹ��ɶ����õ������
��2������EF�����ABP=��������ţ�1������֤�ý��ۣ�
��3������AC��EF��H����BE��AF�Ľ���ΪP���ɵ�E��G�ֱ���AD��CD���е㣬�õ�EG�ǡ�ACD����λ������֤��BE��AC�����ı���ABCD��ƽ���ı��Σ��õ�AD��BC��AD=BC=2$\sqrt{5}$����EAH=��FCH����E��F�ֱ���AD��BC���е㣬�õ�AE=BF=CF=$\frac{1}{2}$AD=$\sqrt{3}$��֤���ı���ABFE��ƽ���ı��Σ�֤��EH=FH���Ƴ�EH��AH�ֱ��ǡ�AFE�����ߣ��ɣ�2���Ľ��۵ü��ɵõ��������������д������Ρ������ã�2�����ۼ��㼴�ɣ�
��� �⣺��1����AF��BE����ABE=45�㣬
��AP=BP=$\frac{\sqrt{2}}{2}$AB=2��
��AF��BE�ǡ�ABC�����ߣ�
��EF��AB��EF=$\frac{1}{2}$AB=$\sqrt{2}$��
���PFE=��PEF=45�㣬
��PE=PF=1��
��Rt��FPB��Rt��PEA��
AE=BF=$\sqrt{{1}^{2}{+2}^{2}}$=$\sqrt{5}$��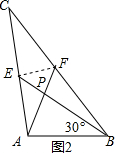
��AC=BC=2$\sqrt{5}$��
��a=b=2$\sqrt{5}$��
��ͼ2������EF��
ͬ���ɵã�EF=$\frac{1}{2}$��4=2��
��EF��AB��
���PEF����ABP��
��$\frac{PF}{AP}=\frac{PE}{PB}=\frac{EF}{AB}=\frac{1}{2}$��
��Rt��ABP��
AB=4����ABP=30�㣬
��AP=2��PB=2$\sqrt{3}$��
��PF=1��PE=$\sqrt{3}$��
��Rt��APE��Rt��BPF��
AE=$\sqrt{7}$��BF=$\sqrt{13}$��
��a=2$\sqrt{13}$��b=2$\sqrt{7}$��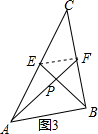
�ʴ�Ϊ��2$\sqrt{5}$��2$\sqrt{5}$��2$\sqrt{13}$��2$\sqrt{7}$��
��2�����룺a2+b2=5c2��
��ͼ3������EF��
���ABP=����
��AP=csin����PB=ccos����
�ɣ�1��ͬ���ɵã�PF=$\frac{1}{2}$PA=$\frac{csin��}{2}$��PE=$\frac{1}{2}PB$=$\frac{ccos��}{2}$��
AE2=AP2+PE2=c2sin2��+$\frac{{{c}^{2}cos}^{2}��}{4}$��BF2=PB2+PF2=$\frac{{{c}^{2}sin}^{2}��}{4}$+c2cos2����
��${��\frac{b}{2}��}^{2}$=c2sin2��+$\frac{{{c}^{2}cos}^{2}��}{4}$��${��\frac{a}{2}��}^{2}$=$\frac{{{c}^{2}sin}^{2}��}{4}$+c2cos2����
��$\frac{{a}^{2}}{4}$+$\frac{{b}^{2}}{4}$=$\frac{{{c}^{2}sin}^{2}��}{4}$+c2cos2��+c2sin2��+$\frac{{{c}^{2}cos}^{2}��}{4}$��
��a2+b2=5c2��
��3����ͼ4������AC��EF����H��AC��BE���ڵ�Q����BE��AF�Ľ���ΪP��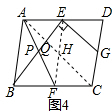
�ߵ�E��G�ֱ���AD��CD���е㣬
��EG��AC��
��BE��EG��
��BE��AC��
���ı���ABCD��ƽ���ı��Σ�
��AD��BC��AD=BC=2$\sqrt{5}$��
���EAH=��FCH��
��E��F�ֱ���AD��BC���е㣬
��AE=$\frac{1}{2}$AD��BF=$\frac{1}{2}$BC��
��AE=BF=CF=$\frac{1}{2}$AD=$\sqrt{5}$��
��AE��BF��
���ı���ABFE��ƽ���ı��Σ�
��EF=AB=3��AP=PF��
�ڡ�AEH�͡�CFH�У�
$\left\{\begin{array}{l}{��EAH=��FCH}\\{��AHE=��FHC}\\{AE=CF}\end{array}\right.$��
���AEH�ա�CFH��
��EH=FH��
��EP��AH�ֱ��ǡ�AFE�����ߣ�
�ɣ�2���Ľ��۵ã�AF2+EF2=5AE2��
��AF2=5${��\sqrt{5��}}^{2}$-EF2=16��
��AF=4��
������F��AB���е�M��֤MF��ֱBP����������д������Ρ�����ΪAB=3��BC=1/2AD=����5��������һ�ʵĽ��ۣ�ֱ�ӿ���AF��
���� ���⿼�������������ε��ж������ʣ����ɶ�����������Ǻ�����ע�����˼���ڱ����е�Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ھ���ABCD�У�AB+1=BC����E��CD����3DE=DC������һ����P�ӵ�A��������·��A��B��C��E�˶������APE�����y���P������·����x֮��ĺ�����ϵ��ͼ�α�ʾ�����ǣ�������
��ͼ���ھ���ABCD�У�AB+1=BC����E��CD����3DE=DC������һ����P�ӵ�A��������·��A��B��C��E�˶������APE�����y���P������·����x֮��ĺ�����ϵ��ͼ�α�ʾ�����ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{��-2��^{2}}$=-2 | B�� | $��\sqrt{9}$=3 | C�� | $\root{3}{64}$=8 | D�� | $\sqrt{{2}^{2}}$=2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ƽ��ֱ������ϵ�У�ֱ��y=-x+2�뷴��������y=$\frac{1}{x}$��ͼ����Ψһ�����㣬��ֱ��y=-x+b�뷴��������y=$\frac{1}{x}$��ͼ����2�������㣬��b��ȡֵ��Χ�ǣ�������
��ƽ��ֱ������ϵ�У�ֱ��y=-x+2�뷴��������y=$\frac{1}{x}$��ͼ����Ψһ�����㣬��ֱ��y=-x+b�뷴��������y=$\frac{1}{x}$��ͼ����2�������㣬��b��ȡֵ��Χ�ǣ�������| A�� | b��2 | B�� | -2��b��2 | C�� | b��2��b��-2 | D�� | b��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2��x��1 | C�� | x��2��x��1 | D�� | x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����̼�����ɫ���С��������������������ܣ�Խ��Խ�����ѡ�������г����°࣮������ij�������г��ϰ�Ӽҳ�������λ�������н��ٶ�v����/���ӣ���ʱ��t�����ӣ��仯�ĺ���ͼ�������ͼ��ʾ��ͼ���������߶�OA��AB��BC��ɣ����߶�OC����һ����T��t��0����ֱ��l��ಿ�ֵ������Ϊt�������������н���·��s���ף���
����̼�����ɫ���С��������������������ܣ�Խ��Խ�����ѡ�������г����°࣮������ij�������г��ϰ�Ӽҳ�������λ�������н��ٶ�v����/���ӣ���ʱ��t�����ӣ��仯�ĺ���ͼ�������ͼ��ʾ��ͼ���������߶�OA��AB��BC��ɣ����߶�OC����һ����T��t��0����ֱ��l��ಿ�ֵ������Ϊt�������������н���·��s���ף����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com