
����Ŀ����֪������OΪԭ���ֱ������ϵ�У������ߵĶ���ΪA ����1����4�����Ҿ�����B����2����3������x��ֱ���C��D���㣮
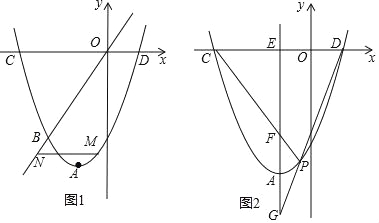
��1����ֱ��OB�Լ�����������Ӧ�ĺ�������ʽ��
��2����ͼ1����M���������ϵ�һ�����㣬����ֱ��OB���·�������M��x���ƽ������ֱ��OB���ڵ�N����MN�����ֵ��
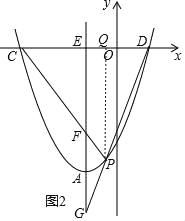
��3����ͼ2������A��ֱ�߽�x���ڵ�E����AE��y�ᣬ��P����������A��D֮���һ�����㣬ֱ��PC��PD��AE�ֱ���F��G���㣮����P�˶�ʱ��EF+EG�Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ���˵�����ɣ�
���𰸡���1��ֱ��OB����ʽΪy=![]() x��������Ϊy=x2+2x��3����2��
x��������Ϊy=x2+2x��3����2��![]() ����3����P�˶�ʱ��EF+EGΪ��ֵ8��
����3����P�˶�ʱ��EF+EGΪ��ֵ8��
��������
�����������1����B���������ô���ϵ��������ֱ��OB����ʽ�����ö���ʽ����������߽���ʽ��
��2����M��t��t2+2t��3����MN=s����ɱ�ʾ��N�����꣬��MN����������ȿɵõ�����s��t�Ĺ�ϵʽ�������ö��κ��������ʿ���������ֵ��
��3����P��t��t2+2t��3������ɱ�ʾ��PQ��CQ��DQ�����������������ε����ʿ���t�ֱ��ʾ��EF��EG�ij����������䶨ֵ��
�����������1����ֱ��OB����ʽΪy=kx��������ɵé�3=��2k�����k=![]() ��
��
��ֱ��OB����ʽΪy=![]() x��
x��
�������߶�������Ϊ����1����4����
�����������߽���ʽΪy=a��x+1��2��4��
�������߾���B����2����3����
����3=a��4�����a=1��
��������Ϊy=x2+2x��3��
��2����M��t��t2+2t��3����MN=s����N�ĺ�����Ϊt��s��������Ϊ![]() ��
��
��MN��x�ᣬ
��t2+2t��3=![]() ����s=
����s=![]() =
=![]() ��
��
����t=![]() ʱ��MN�����ֵ�����ֵΪ
ʱ��MN�����ֵ�����ֵΪ![]() ��
��
��3��EF+EG=8���������£�
��ͼ2������P��PQ��y�ύx����Q��
��y=x2+2x��3�У���y=0�ɵ�0=x2+2x��3�����x=��3��x=1��
��C����3��0����D��1��0����
��P��t��t2+2t��3������PQ=��t2��2t+3��CQ=t+3��DQ=1��t��
��PQ��EF��
���CEF�ס�CQP��
��![]() ��
��
��EF=![]() PQ=
PQ=![]() ����t2��2t+3����
����t2��2t+3����
ͬ����EGD�ס�QPD��![]() ��
��
��EG=![]() PQ=
PQ=![]() ��
��
��EF+EG=![]() ����t2��2t+3��+
����t2��2t+3��+![]() =2����t2��2t+3����
=2����t2��2t+3����![]() ��=2����t2��2t+3����
��=2����t2��2t+3����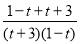 ��=2����t2��2t+3����
��=2����t2��2t+3����![]() ��=8��
��=8��
������P�˶�ʱ��EF+EGΪ��ֵ8��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������y=ax2+bx+c��a��0��ͼ���һ���֣���֪�����ߵĶԳ���Ϊx=2����x���һ�������ǣ���1��0���������н��ۣ�
��abc��0����4a��2b+c��0����4a+b=0������������x�����һ�������ǣ�5��0�������㣨��3��y1������6��y2�������������ϣ�����y1��y2��
������ȷ���ǣ� ��
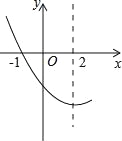
A���٢ڢ� B���ڢܢ� C���٢ۢ� D���ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1���б���٢ڢۢ����ĸ��������У�����y��ԳƵ����������εı��Ϊ______������x��ԳƵ����������εı��Ϊ______����ͼ��2���У�������ABC����x��ԳƵ�ͼ����A1B1C1�����ֱ�д����A1��B1��C1�����꣮
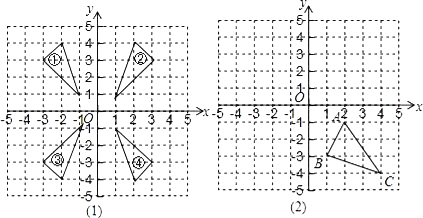
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��Ϊ�෴����c��d��Ϊ������|m|��5�������ʽ2m����a+b��1��+3cd��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⡰��� a b ����ô |a| |b| ������������______________���⣮(��д���桱�١�)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ�ֽ���ȷ������ ��
A. x2-y2=(x-y)2 B. -a+a2=-a(1-a)
C. 4x2-4x+1=4x(x-1)+1 D. a2-4b2=(a+4b)(a -4b)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������2x��-3x2y���Ľ���ǣ�������
A��6x3y B��-6x2y C��-6x3y D��-x3y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ҶԹ�������Դ����ʵ�в������ߣ�2016��ijʡ������Դ�����еġ����ʽ��϶�������������D��ʾ��ʵ��ÿ��3��Ԫ�IJ�����С���Ը�ʡ2016���ϰ��ꡰ���綯���ó��������������ͷֱ���A��B��C��ʾ���͡����ʽ��϶��������������ۼƻ��������о������Ƴ���ͼ��ʾ��������������ͳ��ͼ��

��1����ȫ����ͳ��ͼ��
��2�������D���������ε�Բ�ĽǵĶ�����
��3��Ϊ��һ����ʵ�����ߣ���ʡ�ƻ��ٲ���4.5ǧ��Ԫ�����ƹ������������Ʒ������Ԥ�⣬��ʡ16��ƻ���Լ�����ۡ����ʽ��϶�����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η��̣�x+6��2��9=0�Ľ��ǣ� ��
A.x1=6��x2=��6
B.x1=x2=��6
C.x1=��3��x2=��9
D.x1=3��x2=��9
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com