
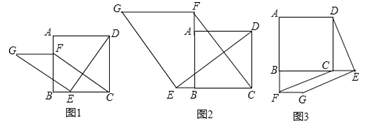
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ��DZ�BC��AB�ϵĵ㣬��CE=BF������DE������E��EG��DE��ʹEG=DE������FG��FC��
��1�����жϣ�FG��CE��������ϵ�� ��λ�ù�ϵ�� ��
��2����ͼ2������E��F�ֱ��DZ�CB��BA�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ�������������жϲ�����֤����
��3����ͼ3������E��F�ֱ��DZ�BC��AB�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ��������ֱ��д������ж���
���𰸡���1��FG=CE��FG��CE����2����������3��������
��������
�����������1��ֻҪ֤���ı���CDGF��ƽ���ı��μ��ɵó�FG=CE��FG��CE��
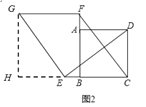
��2�����츨���ߺ�֤����HGE�ա�CED�����ö�Ӧ�������֤�ı���GHBF�Ǿ��κ����õ��������������FG=C��FG��CE��
��3��֤����CBF�ա�DCE����֤���ı���CEGF��ƽ���ı��Σ�
�����������1��FG=CE��FG��CE��
��2������G��GH��CB���ӳ����ڵ�H����EG��DE�����GEH+��DEC=90�㣬�ߡ�GEH+��HGE=90�㣬���DEC=��HGE���ڡ�HGE���CED�У��ߡ�GHE=��DCE����HGE=��DEC��EG=DE�����HGE�ա�CED��AAS������GH=CE��HE=CD����CE=BF����GH=BF����GH��BF�����ı���GHBF�Ǿ��Σ���GF=BH��FG��CH����FG��CE�����ı���ABCD�������Σ���CD=BC����HE=BC����HE+EB=BC+EB����BH=EC����FG=EC��
��3�����ı���ABCD�������Σ���BC=CD����FBC=��ECD=90�㣬�ڡ�CBF���DCE�У���BF=CE����FBC=��ECD��BC=DC�����CBF�ա�DCE��SAS�������BCF=��CDE��CF=DE����EG=DE����CF=EG����DE��EG�����DEC+��CEG=90�����ߡ�CDE+��DEC=90�������CDE=��CEG�����BCF=��CEG����CF��EG�����ı���CEGFƽ���ı��Σ���FG��CE��FG=CE��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�κ���y����2x+1������˵����ȷ���ǣ�������
A.ͼ��ֲ��ڵ�һ������������
B.y��x�����������
C.ͼ���㣨1����2��
D.����A��x1��y1����B��x2��y2������ͼ���ϣ���x1��x2����y1��y2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A=65�㣬���A�IJ��ǵ��ڣ�������
A.125��
B.105��
C.115��
D.95��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2+ax��2a��0��һ������3����������һ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����4�·ݵIJ�ֵ��500��Ԫ����5�·�����¼������Ľ�����������ڶ����ȵIJ�ֵ����1655��Ԫ��5��6�·�ƽ��ÿ�µ���������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
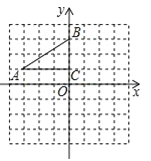
����Ŀ������2016�Ĵ�ʡ��֦���У���ͼ����ƽ��ֱ������ϵ�У�ֱ�ǡ�ABC����������ֱ���A����3��1����B��0��3����C��0��1��
��1������ABC�Ե�CΪ��ת������ת180�㣬������ת���Ӧ�ġ�A1B1C1��
��2���ֱ�����AB1��BA1�����ı���AB1A1B�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
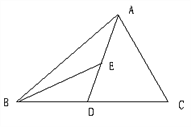
����Ŀ����ͼ��ADΪ��ABC�����ߣ�BEΪ��ABD�����ߣ�
��1����ABE=15�㣬��BAD=40�㣬���BED�Ķ�����
��2������BED�ı�BD���ϵĸߣ�
��3������ABC�����Ϊ40��BD=5�����BDE ��BD���ϵĸ�Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��DE��BC������Ϊ��E������AC��DE�ڵ�F����GΪAF���е㣬��ACD=2��ACB����DG=3��EC=1����DE�ij�Ϊ�� ��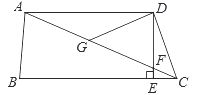
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com