练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．下列命题错误的是（　　）
    A．平行四边形的对角相等B．正方形的对角线相等
    C．对角线相等的平行四边形是矩形D．对角线互相垂直的四边形是菱形

    分析 分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案．

    解答 解：A、平行四边形的对角相等，是真命题，故本选项错误；
    B、正方形的对角线相等，是真命题，故本选项错误，
    C、对角线相等的平行四边形是矩形，是真命题，故本选项错误；
    D、对角线互相垂直的平行四边形是菱形，故本选项错误，
    故选D．

    点评 本题主要考查了命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

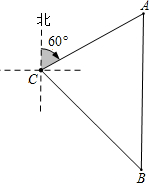    5．在甲、乙两地之间需修一南北走向的隧道AB．从入口B的西北方向600米的C点处，测得另一入口A在C点的北偏东60°的方向上，求隧道AB的长（最后结果保留整数）．（参考数据：$\sqrt{2}≈1.414\;，\sqrt{3}≈1.732，\sqrt{6}$≈2.449）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知x2-2x-8=0，求4（x-1）2-2x（x-2）+3的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．（1）如图1，G是△ABC的重心，AG，BG，CG的延长线分别交BC，AC，AB于点D，E，F，$\frac{AG}{GD}+\frac{BG}{GE}+\frac{CG}{GF}$的值为6；
    （2）如图2，G是△ABC的重心．∠ACB＞90°，连接AG，BG，CG，①当∠AGC=90°，证明：BG=AC；
    （3）设G是△ABC的重心，BC=a，AC=b，AB=c，当△ACG为直角三角形时，请直接写出a，b，c之间的数量关系．

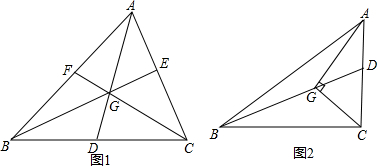
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．已知：a、b是常数，若关于m、n的二元一次方程组$\left\{\begin{array}{l}{am+bn=9.1}\\{3am+2bn=6.7}\end{array}\right.$的解是$\left\{\begin{array}{l}{m=3.1}\\{n=1.7}\end{array}\right.$，则关于x、y的二元一次方程组$\left\{\begin{array}{l}{a（x+1）+b（y-2）=9.1}\\{3a（x+1）+2b（y-2）=6.7}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2.1}\\{y=3.7}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．（1）解方程：x2-6x+8=0；
    （2）解不等式组：$\left\{\begin{array}{l}{2（x-1）≥x+1}\\{x-2＞\frac{1}{3}（2x-1）}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：
    （1）（7+4$\sqrt{3}$）（2-$\sqrt{3}$）2+（2+$\sqrt{3}$）（2-$\sqrt{3}$）-$\sqrt{3}$
    （2）$10{a^2}\sqrt{ab}•5\sqrt{\frac{b}{a}}÷15\sqrt{\frac{a}{b}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知关于x，y的方程组$\left\{\begin{array}{l}2x-3y=2\\ mx+2y=5\end{array}\right.$的解是方程x-2y=3的解，求出m 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．若把分$\frac{2xy}{2x+y}$中的x和y都扩大3倍，那么分式的值（　　）
    A．扩大3倍B．不变C．缩小3倍D．扩大9倍

    查看答案和解析>>

    同步练习册答案