


科目:初中数学 来源: 题型:
 已知:正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点M.
已知:正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为( )
如图,△ACF内接于⊙O,AB是⊙O直径,弦CD⊥AB于E,若CD=BE=8,则sin∠AFC的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知Rt△ABC,∠C=90°,CA=3,CB=4,点M从点B出发沿线段BC匀速运动至点C,过点M作MN⊥AB于N,则△BMN面积S与点M的运动时间t之间的函数图象大致是( )
如图,已知Rt△ABC,∠C=90°,CA=3,CB=4,点M从点B出发沿线段BC匀速运动至点C,过点M作MN⊥AB于N,则△BMN面积S与点M的运动时间t之间的函数图象大致是( )A、 |
B、 |
C、 |
D、 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 一艘轮船沿长江顺流从武汉开往上海,行驶6小时后,发现船上一救生艇掉入江中,然后立即返回,再行驶3小时碰见救生艇.下图是轮船离出发地的距离与时间的函数关系,已知水流速度为5千米/时,则救生艇在轮船出发
一艘轮船沿长江顺流从武汉开往上海,行驶6小时后,发现船上一救生艇掉入江中,然后立即返回,再行驶3小时碰见救生艇.下图是轮船离出发地的距离与时间的函数关系,已知水流速度为5千米/时,则救生艇在轮船出发查看答案和解析>>
科目:初中数学 来源: 题型:
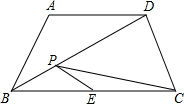 如图所示,在等腰梯形ABCD中,AD∥BC,∠A=120°,AB=AD=2,点E是BC的中点,点P是对角线BD上的动点,则PE+PC的最小值是( )
如图所示,在等腰梯形ABCD中,AD∥BC,∠A=120°,AB=AD=2,点E是BC的中点,点P是对角线BD上的动点,则PE+PC的最小值是( )| A、2 | ||
B、2
| ||
C、2
| ||
| D、3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com