
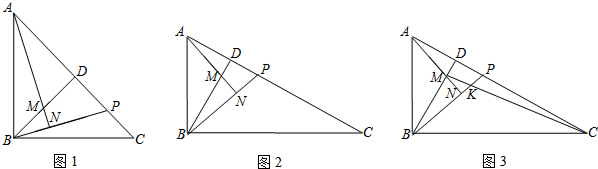
分析 (1)利用等腰直角三角形的性质和全等三角形的判定定理可得△ABM≌△BCP,易得BM=CP;
(2)首先证明△AMB∽△BPC,利用相似三角形的性质易得$\frac{BM}{CP}=\frac{AB}{BC}$,由特殊角的三角函数易得$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$,易得出结论;
(3)连接MP,由DP=$\frac{1}{4}$PC=3,易得CP=12,CD=15,BD=5$\sqrt{3}$,BM=4$\sqrt{3}$,DM=$\sqrt{3}$,CM=2$\sqrt{57}$,证得△DMP∽△DBC,△MKP∽△CKB,利用相似三角形的性质,得$\frac{MK}{CK}$,求得MK的长.
解答 (1)证明:∵∠ABC=90°,∠C=45°,
∴∠BAC=45°,
∴AB=AC,
∵BD⊥AC,
∴∠ABD=45°,∠CBD=∠45°,
∴∠ABD=∠C=∠CBD,
∵AN⊥BP,BD⊥AC,
∴∠MAD=∠MBN,
∴∠MAB=∠PBC,
在△ABM与△BCP中,
$\left\{\begin{array}{l}{∠MAB=∠PBC}\\{AB=CB}\\{∠ABM=∠C}\end{array}\right.$,
∴△ABM≌△BCP(SAS),
∴BM=CP;
(2)解:∵BD⊥AC,∠ABC=90°,
即∠ABD+∠DBC=90°,∠BAD+∠ABD=90°,
∴∠DBC=∠BAD,
由(1)∠DAN=∠DBN,
∴∠MAB=∠PBC,
∵BD⊥AC,AN⊥BP,
∴∠DMN+∠DPN=180°,
∵∠DPN+∠BPC=180°,
∴∠DMN=∠BPC,
∵∠DMN=∠AMB,
∴∠BPC=∠AMB,
∵∠MAB=∠PBC,
∴△AMB∽△BPC,
∴$\frac{BM}{CP}=\frac{AB}{BC}$,
∵∠C=30°,
∴tan∠C=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{BM}{CP}=\frac{\sqrt{3}}{3}$,
∴CP=$\sqrt{3}BM$,
故答案为:CP=$\sqrt{3}$BM;
(3)解:连接MP,由DP=$\frac{1}{4}$PC=3,可得CP=12,CD=15,BD=5$\sqrt{3}$,BM=4$\sqrt{3}$,DM=$\sqrt{3}$,CM=2$\sqrt{57}$,
∵$\frac{DM}{DB}=\frac{DP}{CD}=\frac{1}{5}$,∠BDC=∠MDP,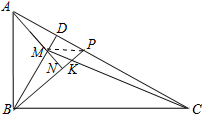
∴△DMP∽△DBC,
∴∠DMP=∠DBC,
∴MP∥BC,
∴△MKP∽△CKB,
∴$\frac{MK}{CK}=\frac{MP}{BC}=\frac{1}{5}$,
∴$\frac{MK}{MC}$=$\frac{1}{6}$,
∴MK=$\frac{1}{6}$MC=$\frac{1}{6}$×$2\sqrt{57}$=$\frac{\sqrt{57}}{3}$.
点评 本题主要考查了全等三角形的判定及性质与相似三角形的判定及性质,锐角三角函数等,利用角的关系找到相似三角形的判定条件是解答此题的关键.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
| 饮料 | 果汁饮料 | 碳酸饮料 |
| 进价(元/箱) | 51 | 36 |
| 售价(元/箱) | 61 | 43 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
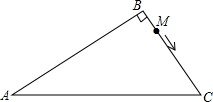 如图,在Rt△ABC中,∠B=90°,AB=2$\sqrt{3}$cm,AC=4cm,动点M从点B出发以每秒$\sqrt{2}$cm的速度沿B→C→A方向移动到点A,则点M出发几秒后,可使△ABC的面积是△ABM面积的4倍?
如图,在Rt△ABC中,∠B=90°,AB=2$\sqrt{3}$cm,AC=4cm,动点M从点B出发以每秒$\sqrt{2}$cm的速度沿B→C→A方向移动到点A,则点M出发几秒后,可使△ABC的面积是△ABM面积的4倍?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com