
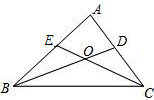
 △ABC中,∠ABC、∠ACB的平分线相交于点O;
△ABC中,∠ABC、∠ACB的平分线相交于点O; (40°+50°)=135°;
(40°+50°)=135°; ×116°=122°;
×116°=122°; ×(180°-∠A)=128°;
×(180°-∠A)=128°; (∠ABC+∠ACB)
(∠ABC+∠ACB) (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠A)=90°+0.5x.
(180°-∠A)=90°+0.5x. ∠A.
∠A. 

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
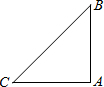 20、问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.探究∠DBC与∠ABC度数的比值.
20、问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.探究∠DBC与∠ABC度数的比值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:江苏期中题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:湖南省中考真题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com