
【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于50棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
【答案】
(1)解:设购买A种树苗每棵需要x元,B种树苗每棵需要y元,
由已知得: ![]() ,
,
解得: ![]() .
.
答:购买A种树苗每棵需要100元,B种树苗每棵需要50元
(2)解:设购买A种树苗m棵,则购买B种树苗100﹣m棵,
根据已知,得 ![]() ,
,
解得:50≤m≤53.
故有四种购买方案:1、购买A种树苗50棵,B种树苗50棵;2、购买A种树苗51棵,B种树苗49棵;3、购买A种树苗52棵,B种树苗48棵;4、购买A种树苗53棵,B种树苗47棵
(3)解:设种植工钱为W,由已知得:
W=30m+20(100﹣m)=10m+2000,
∴当m=50时,W最小,最小值为2500元.
故购买A种树苗50棵、B种树苗50棵时所付的种植工钱最少,最少工钱是2500元.
【解析】(1)设购买A种树苗每棵需要x元,B种树苗每棵需要y元,根据总价=单价×数量,可列出关于x、y的二元一次方程组,解方程组即可得出结论;(2)设购买A种树苗m棵,则购买B种树苗100﹣m棵,根据总价=单价×数量,可列出关于m的一元一次不等式组,解不等式组即可得出m的取值范围,由此可得出结论;(3)设种植工钱为W,根据植树的工钱=植A种树的工钱+植乙种数的工钱,列出W关于m的函数关系式,根据一次函数的单调性即可解决最值问题.


科目:初中数学 来源: 题型:
【题目】如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=110°,则∠1+∠2的度数为( )

A. 80°; B. 90°; C. 100°; D. 110°;
查看答案和解析>>
科目:初中数学 来源: 题型:
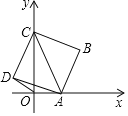
【题目】如图,点A是x轴上的一个动点,点C在y轴上,以AC为对角线画正方形ABCD,已知点C的坐标是![]() ,设点A的坐标为
,设点A的坐标为![]() .
.
![]() 当
当![]() 时,正方形ABCD的边长
时,正方形ABCD的边长![]() ______.
______.
![]() 连结OD,当
连结OD,当![]() 时,
时,![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=57.65°,则∠AOD的度数是( )
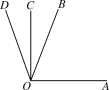
A. 122°20′ B. 122°21′ C. 122°22′ D. 122°23′
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定运算符号的意义是:当a>b时,ab=a﹣b;当a<b时,ab=a+b.
(1)计算:61= ;(﹣3)2= ;
(2)棍据运算符号的意义且其他运算符号意义不变的条件下,
①计算:﹣14+15×[(﹣![]() )(﹣
)(﹣![]() )]﹣(3223)÷(﹣7),
)]﹣(3223)÷(﹣7),
②若x,y在数轴上的位置如图所示,
a.填空:x2+1 y(填“>“或“<”):
b.化简:[(x2+x+1)(x+y)]+[(y﹣x2)(y+2)].
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在篮球比赛中,某队员连续10场比赛中每场的得分情况如下所示:
场次(场) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分(分) | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 18 |
则这10场比赛中该队员得分的中位数和众数分别是( )
A.10,4
B.10,13
C.11,4
D.12.5,13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+2经过A(﹣1,0),B(2,0),C三点.直线y=mx+ ![]() 交抛物线于A,Q两点,点P是抛物线上直线AQ上方的一个动点,作PF⊥x轴,垂足为F,交AQ于点N.
交抛物线于A,Q两点,点P是抛物线上直线AQ上方的一个动点,作PF⊥x轴,垂足为F,交AQ于点N.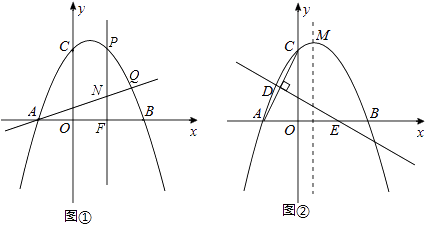
(1)求抛物线的解析式;
(2)如图①,当点P运动到什么位置时,线段PN=2NF,求出此时点P的坐标;
(3)如图②,线段AC的垂直平分线交x轴于点E,垂足为D,点M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
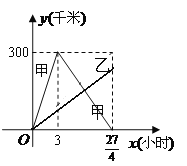
【题目】已知:甲、乙两车分别从相距300千米的 A,B两地同时出发相向而行,其中甲到 B地后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离 y(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)当它们行驶到与各自出发地的距离相等时,用了 ![]() 小时,求乙车离出发地的距离 y(千米)与行驶时间 x(小时)之间的函数关系式;
小时,求乙车离出发地的距离 y(千米)与行驶时间 x(小时)之间的函数关系式;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com