
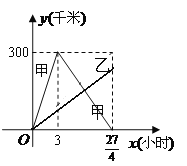
����Ŀ����֪���ס��������ֱ�����300ǧ�� A,B����ͬʱ����������У����м� B�غ��������أ���ͼ����������Գ����صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ���ͼ����
��1����׳�������صľ��� y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��2����������ʻ������Գ����صľ������ʱ������ ![]() Сʱ�����ҳ�������صľ��� y��ǧ�ף�����ʻʱ�� x��Сʱ��֮��ĺ�����ϵʽ��
Сʱ�����ҳ�������صľ��� y��ǧ�ף�����ʻʱ�� x��Сʱ��֮��ĺ�����ϵʽ��
��3���ڣ�2���������£�����������ʻ�Ĺ�����������ʱ�䣮
���𰸡�������
��������������
��1����ͼ֪���ú�����ϵ�ڲ�ͬ��ʱ������ֳɲ�ͬ�Ĺ�ϵ����ֶα������ʻʱ��С��3ʱ������������������ʹʱ�����3С��![]() ʱ��һ�κ������ɸ��ݴ���ϵ�����з��̣�������ϵʽ��
ʱ��һ�κ������ɸ��ݴ���ϵ�����з��̣�������ϵʽ��
��2��4.5Сʱ����3������һ�κ�����ϵʽ��������ҳ�������![]() Сʱ��ʹ�ľ��룮��ͼ��ɿ������ҳ�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮����������������ϵ���ô���ϵ��������⣮
Сʱ��ʹ�ľ��룮��ͼ��ɿ������ҳ�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮����������������ϵ���ô���ϵ��������⣮
��3������������У�����ʱ�ס���������ʹ�ľ���֮��Ϊ300ǧ�ף��г����̽��������������������
��⣺
��1����1����0��x��3ʱ������������������Ϊy=kx��
x=3ʱ��y=300��������k=100������y=100x��
��3��x��![]() ʱ����һ�κ�������Ϊy=kx+b��
ʱ����һ�κ�������Ϊy=kx+b��
�������㣨3��300������![]() ��0������
��0������
���![]() ��
��
����y=540��80x��
�ۺ����ϵü׳�������صľ���y����ʻʱ��x֮��ĺ�����ϵʽ Ϊ��y= ��
��
��2����x=![]() ʱ��y��=540��80��
ʱ��y��=540��80��![]() =180��
=180��
�ҳ����㣨![]() ��180����y��=40x����0��x��
��180����y��=40x����0��x��![]() ��
��
��3��������������������
�ٵ�0��x��3��100x+40x=300�����x=![]() ��
��
�ڵ�3��x��![]() ʱ����540��80x��+40x=300�����x=6��
ʱ����540��80x��+40x=300�����x=6��
����������������һ������ʱ��Ϊ��![]() Сʱ���ڶ�������ʱ��Ϊ��6Сʱ��
Сʱ���ڶ�������ʱ��Ϊ��6Сʱ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڴ���ȫ���������й����У���������A��B���������ij·�ε�·�����̻����죬��֪����A������8�ã�B������3�ã���Ҫ950Ԫ��������A������5�ã�B������6�ã�����Ҫ800Ԫ��
��1������A��B��������ÿ�ø������Ԫ��
��2�����ǵ��̻�Ч�����ʽ���ת������A�����粻������50�ã������ڹ���������������ʽ��ܳ���7650Ԫ�����������������繲100�ã������ļ��ֹ�����
��3��ij�����ӳа���ֲ�������ֺ�һ��A������ɻ�Ǯ30Ԫ���ֺ�һ��B������ɻ�Ǯ20Ԫ���ڵڣ�2���ʵĸ��ֹ����У��ֺ���100�����磬��һ�ֹ�����������ֲ��Ǯ���٣����ٹ�Ǯ�Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
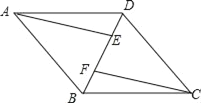
����Ŀ����֪����ͼ���ı���ABCD��ƽ���ı��Σ�AE��CF���ҷֱԽ���BD�ڵ�E��F��
��1����֤����AEB�ա�CFD��
��2������AF��CE������AFE=��CFE����֤���ı���AFCE�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y= ![]() ��ͼ��λ�ڵڶ����������ޣ���ô����x��һԪ���η���x2+2x+k=0�ĸ�������ǣ� ��
��ͼ��λ�ڵڶ����������ޣ���ô����x��һԪ���η���x2+2x+k=0�ĸ�������ǣ� ��
A.��������������ȵ�ʵ����
B.���̲�һ����ʵ����
C.������������ȵ�ʵ����
D.����û��ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O��ֱ��CD=10��AB�ǡ�O���ң�AB��CD������ΪM����AB=8����AC�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����˳ɳ���Ӱ���Ǿ�ģ�һ�����������ܸı��˵�һ����ÿ���4��23�ձ����Ϲ��̿�����֯ȷ��Ϊ�������������ijУ��ѧ�꿪չ�˶���������λ�У����꼶![]() ��40��ѧ�����������������
��40��ѧ�����������������
������� | 4 | 5 | 6 | 7 | 8 |
���� | 6 | 4 | 10 | 12 | 8 |
���ݱ��е����ݣ���
(1)�ð�ѧ�����������ƽ������
(2)�ð�ѧ�������������λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD���ڵ�O����DE��AC��CE��BD��
��1����֤���ı���OCED�����Σ�
��2������BAC=30�㣬AC=4��������OCED�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ����Բ���������ڷ���һ��ʵ�ĵġ����塱����һ��Բ����һ��ͬ�����Բ��ɵļ����壩�������������������עˮ��ˮ���ٶ�Ϊ5cm3/s��ע��Ϊֹ����֪����עˮ�����У�ˮ��߶�h��cm����עˮʱ��t��s��֮��Ĺ�ϵ��ͼ����ʾ���������ͼ����Ϣ������������⣺ 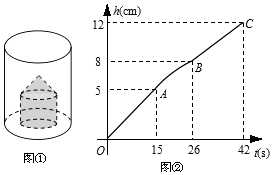
��1��Բ���������ĸ�Ϊcm�������塱��Բ��ĸ�Ϊcm��
��2���ֱ����Բ���������ĵ�����롰���塱�ĵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������![]() ������������Щ������ʹ�������������磺
������������Щ������ʹ�������������磺 ![]() �����dz�ʹ��
�����dz�ʹ��![]() ������һ����
������һ����![]() ,
, ![]() Ϊ��������ԡ�����Ϊ
Ϊ��������ԡ�����Ϊ![]() ��
��
��1����![]() �ǡ�������ԡ�����
�ǡ�������ԡ�����![]() ��ֵ��
��ֵ��
��2��д��һ����������ԡ� ![]() ������
������![]() ��
��![]() ��
��
��3����![]() �ǡ�������ԡ��������ʽ
�ǡ�������ԡ��������ʽ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com