
【题目】如图所示,在∠AOB的两边上截取AO=BO,OC=OD,连接AD、BC交于点P,连接OP,则下列结论正确的是 ( )
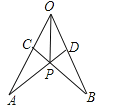
①△APC≌△BPD ②△ADO≌△BCO ③△AOP≌△BOP ④△OCP≌△ODP
A. ②③④ B. ①②③ C. ①②③④ D. ①③④
【答案】C
【解析】由AO=BO,OC=OD,∠O=∠O,可证得②△ADO≌△BCO,所以有∠COP=∠DOP,又OC=OD,OP=OP,可证得④△OCP≌△ODP,所以有PC=PD,又∠CAP=∠DBP,∠CPA=∠DBP可证得① △APC≌△BPO,所以有PA=PB,又AO=BO,OP=OP,可证得③ △AOP≌△BOP.
解:∵AO=BO,OC=OD,∠O=∠O,
∴△ADO≌△BCO(SAS),故②正确;
∴∠COP=∠DOP,
∵OC=OD,OP=OP,
∴△OCP≌△ODP(SAS),故④正确;
∴PC=PD,
∵∠CAP=∠DBP,∠CPA=∠DPB,
∴△APC≌△BPD(AAS),故①正确;
∴PA=PB,
∵AO=BO,OP=OP,
∴△AOP≌△BOP(SSS),故③正确.
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为_____.
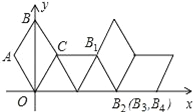
查看答案和解析>>
科目:初中数学 来源: 题型:
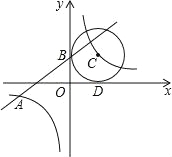
【题目】(2016浙江省舟山市第21题)如图,已知一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=
的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数y2=![]() 的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
(1)、求m的值;
(2)、求一次函数的表达式;
(3)、根据图象,当y1<y2<0时,写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com