
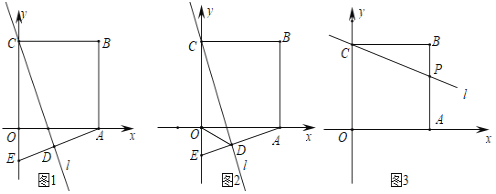
【题目】如图,正方形OABC的顶点O是坐标原点,边OA和OC分别在x轴、y轴上,点B的坐标为(4,4).直线l经过点C.
(1)若直线l与边OA交于点M,过点A作直线l的垂线,垂足为D,交y轴于点E.
①如图1,当OE=1时,求直线l对应的函数表达式;
②如图2,连接OD,求证:OD平分∠CDE.
(2)如图3,若直线l与边AB交于点P,且S△BCP=![]() S四边形AOCP,此时,在x轴上是否存在点Q,使△CPQ是以CP为直角边的直角三角形?若存在,求点Q的坐标,若不存在,请说明理由.
S四边形AOCP,此时,在x轴上是否存在点Q,使△CPQ是以CP为直角边的直角三角形?若存在,求点Q的坐标,若不存在,请说明理由.
【答案】(1)①y=﹣4x+4;②见解析;(2)存在,点Q(3,0)或(﹣2,0)
【解析】
(1)①由题意可求点A,点C坐标,用待定系数法可求直线AE解析式,由AE⊥直线l,可设直线l的解析式为y=﹣4x+m,将点C坐标代入,可求直线l的解析式;
②连接AC,由∠AOC=∠ADC=90°,可得点C,点A,点D,点O四点共圆,可得∠CAO=∠ODC=45°,即OD平分∠CDE;
(2)分∠PCQ=90°和∠CPQ=90°两种情况讨论,根据全等三角形的性质和相似三角形的性质可求点Q的坐标.
解:(1)①∵四边形OABC是正方形,点B(4,4)
∴点A(4,0),点C(0,4),
∴AO=CO=AB=BC=4,
∵OE=1
∴点E(0,﹣1)
设直线AE解析式为:y=kx+b,
∴![]()
解得:k=![]() ,b=﹣1,
,b=﹣1,
∴直线直线AE解析式为y=![]() x﹣1,
x﹣1,
∵AE⊥直线l,
∴设直线l的解析式为y=﹣4x+m,且过点C(0,4)
∴m=4,
∴直线l的解析式为y=﹣4x+4
②如图,连接AC,
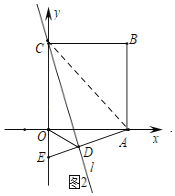
∵四边形OABC是正方形,
∴∠COA=90°,∠CAO=45°,
∵∠COA=∠CDA=90°,
∴点C,点A,点D,点O四点共圆,
∴∠CAO=∠ODC=45°
∴∠ODC=![]() ∠CDE
∠CDE
∴OD平分∠CDE
(2)存在
∵S△BCP=![]() S四边形AOCP,
S四边形AOCP,
∴S△BCP=![]() S正方形OABC,
S正方形OABC,
∴![]() ×4×BP=
×4×BP=![]() ×4×4,
×4×4,
∴BP=2,
∴AP=AB﹣BP=2,
如图,若∠PCQ=90°,
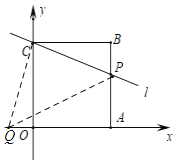
∴∠QCO+∠OCP=90°,
又∵∠BCO=∠BCP+∠OCP=90°,
∴∠QCO=∠BCP,且BC=CO,∠COQ=∠B=90°,
∴△BCP≌△OCQ(ASA)
∴BP=OQ=2
∴点Q(﹣2,0)
如图,若∠CPQ=90°,
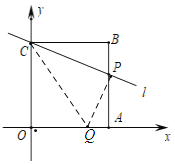
∴∠APQ+∠BPC=90°,
又∵∠BPC+∠BCP=90°,
∴∠BCP=∠APQ,且∠B=∠PAQ=90°,
∴△APQ∽△BCP
∴![]()
∴![]()
∴AQ=1,
∴OQ=AO﹣AQ=3,
∴点Q(3,0)
综上所述:点Q(3,0)或(﹣2,0)


科目:初中数学 来源: 题型:
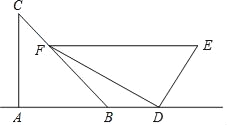
【题目】小华是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A,B,D在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=2![]() .则BD=_____.
.则BD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
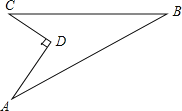
【题目】如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米300元,试问用该草坪铺满这块空地共需花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决问题:
我们把一个能被17整除的自然数称为“节俭数”,“节俭数”的特征是:若把一个自然数的个位数字截去,再把剩下的数减去截去的那个个位数字的5倍,如果差是17的整数倍(包括0),则原数能被17整除.如果差太大或心算不易看出是否是17的倍数,就继续上述的“截尾、倍大、相减、验差”的过程,直到能清楚判断为止.
例如:判断1675282是不是“节俭数”.判断过程:167528﹣2×5=167518,16751﹣8×5=16711,1671﹣1×5=1666,166﹣6×5=136,到这里如果你仍然观察不出来,就继续13﹣6×5=﹣17,﹣17是17的整数倍,所以1675282能被17整除.所以1675282是“节俭数”.
(1)请用上述方法判断7259和2098752 是否是“节俭数”,并说明理由;
(2)一个五位节俭数![]() ,其中个位上的数字为b,十位上的数字为a,请求出这个数.
,其中个位上的数字为b,十位上的数字为a,请求出这个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误的有( )
①在Rt△ABC中,已知两边长分别为3和4,则第三边的长为5;
②△ABC的三边长分别为AB,BC,AC,若![]() +
+![]() =
=![]() ,则∠A=90°;
,则∠A=90°;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④若三角形的三边长之比为3:4:5,则该三角形是直角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有三点A(﹣2,1)、B(3,1)、C(2,3).请回答如下问题:
(1)在坐标系内描出点A、B、C的位置,并求△ABC的面积;
(2)在平面直角坐标系中画出△A′B′C′,使它与△ABC关于x轴对称,并写出△A′B′C′三顶点的坐标;
(3)若M(x,y)是△ABC内部任意一点,请直接写出这点在△A′B′C′内部的对应点M′的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com