
【题目】用大小相等的小正方形按一定规律拼成下列图形,则第n个图形中小正方形的个数是( ) 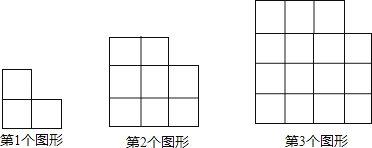
A.2n+1
B.n2﹣1
C.n2+2n
D.5n﹣2
科目:初中数学 来源: 题型:
【题目】某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.
时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |
另一部分鲜花在淘宝网销售,网上销售日销售量y2(万朵)与时间x(x为整数,单位:天) 关系如图所示.
(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与x的变化规律,写出y1与x的函数关系式及自变量x的取值范围;
(2)观察马蹄莲网上销售量y2与时间x的变化规律,请你设想商家采用了何种销售策略使得销售量发生了变化,并写出销售量y2与x的函数关系式及自变量x的取值范围;
(3)设该花木公司日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生课外小组活动,培养学生动手操作能力,王老师让学生把5m长的彩绳截成2m或1m的彩绳,用来做手工编织,在不造成浪费的前提下,你有几种不同的截法( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:
如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE= ![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC= ![]() CD.
CD.
简单应用:
(1)在图①中,若AC= ![]() ,BC=2
,BC=2 ![]() ,则CD= .
,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙上, ![]() =
= ![]() ,若AB=13,BC=12,求CD的长.
,若AB=13,BC=12,求CD的长.
拓展规律:
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示)
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE= ![]() AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了图形的旋转知识后,数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究. 
(一)尝试探究
如图1,在四边形ABCD中,AB=AD,∠BAD=60°,∠ABC=∠ADC=90°,点E、F分别在线段BC、CD上,∠EAF=30°,连接EF.
(1)如图2,将△ABE绕点A逆时针旋转60°后得到△A′B′E′(A′B′与AD重合),请直接写出∠E′AF=度,线段BE、EF、FD之间的数量关系为 .
(2)如图3,当点E、F分别在线段BC、CD的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为调查本校学生周末平均每天做作业所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分.

请根据以上信息,解答下列问题:
(1)在这次调查的数据中,做作业所用时间的众数是 ,中位数是 ,平均数是 ;
(2)若该校共有2000名学生,根据以上调查结果估计该校全体学生每天做作业时间在3小时内(含3小时)的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB﹣BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND﹣DC﹣CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t秒,则S与t函数关系的大致图象为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市政府计划投资1.4万亿元实施东进战略.为了解深圳市民对东进战略的关注情况.某校数学兴趣小组随机采访部分深圳市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | M | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | N |
D.不知道 | 50 | 0.25 |

(1)根据上述统计图可得此次采访的人数为人,m= , n=
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在15000名深圳市民中,高度关注东进战略的深圳市民约有人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com