
【题目】已知抛物线y=x2+bx+c(b,c是常数)与x轴相交于A,B两点(A在B的左侧),与y轴交于点C.
(1)当A(﹣1,0),C(0,﹣3)时,求抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点.
①当点P关于原点的对称点P′落在直线BC上时,求m的值;
②当点P关于原点的对称点P′落在第一象限内,P′A2取得最小值时,求m的值及这个最小值.
【答案】(1)抛物线的解析式为y=x2﹣2x﹣3,顶点坐标为(1,﹣4);(2)①m=![]() ;②P′A2取得最小值时,m的值是
;②P′A2取得最小值时,m的值是![]() ,这个最小值是
,这个最小值是![]() .
.
【解析】
(1)根据A(﹣1,0),C(0,﹣3)在抛物线y=x2+bx+c(b,c是常数)的图象上,可以求得b、c的值;
(2)①根据题意可以得到点P′的坐标,再根据函数解析式可以求得点B的坐标,进而求得直线BC的解析式,再根据点P′落在直线BC上,从而可以求得m的值;
②根据题意可以表示出P′A2,从而可以求得当P′A2取得最小值时,m的值及这个最小值.
(1)∵抛物线y=x2+bx+c(b,c是常数)与x轴相交于A,B两点,与y轴交于点C,A(﹣1,0),C(0,﹣3),∴![]() ,解得:
,解得:![]() ,∴该抛物线的解析式为y=x2﹣2x﹣3.
,∴该抛物线的解析式为y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的顶点坐标为(1,﹣4);
(2)①由P(m,t)在抛物线上可得:t=m2﹣2m﹣3.
∵点P和P′关于原点对称,∴P′(﹣m,﹣t),当y=0时,0=x2﹣2x﹣3,解得:x1=﹣1,x2=3,由已知可得:点B(3,0).
∵点B(3,0),点C(0,﹣3),设直线BC对应的函数解析式为:y=kx+d,![]() ,解得:
,解得:![]() ,∴直线BC的直线解析式为y=x﹣3.
,∴直线BC的直线解析式为y=x﹣3.
∵点P′落在直线BC上,∴﹣t=﹣m﹣3,即t=m+3,∴m2﹣2m﹣3=m+3,解得:m=![]() ;
;
②由题意可知,点P′(﹣m,﹣t)在第一象限,∴﹣m>0,﹣t>0,∴m<0,t<0.
∵二次函数的最小值是﹣4,∴﹣4≤t<0.
∵点P(m,t)在抛物线上,∴t=m2﹣2m﹣3,∴t+3=m2﹣2m,过点P′作P′H⊥x轴,H为垂足,有H(﹣m,0).
又∵A(﹣1,0),则P′H2=t2,AH2=(﹣m+1)2.在Rt△P′AH中,P′A2=AH2+P′H2,∴P′A2=(﹣m+1)2+t2=m2﹣2m+1+t2=t2+t+4=(t+![]() )2+
)2+![]() ,∴当t=﹣
,∴当t=﹣![]() 时,P′A2有最小值,此时P′A2=
时,P′A2有最小值,此时P′A2=![]() ,∴
,∴![]() =m2﹣2m﹣3,解得:m=
=m2﹣2m﹣3,解得:m=![]() .
.
∵m<0,∴m=![]() ,即P′A2取得最小值时,m的值是
,即P′A2取得最小值时,m的值是![]() ,这个最小值是
,这个最小值是![]() .
.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】为做好食堂的服务工作,某学校食堂对学生最喜爱的菜肴进行了抽样调查,下面试根据收集的数据绘制的统计图(不完整):
(1)参加抽样调查的学生数是______人,扇形统计图中“大排”部分的圆心角是______°;
(2)把条形统计图补充完整;
(3)若全校有3000名学生,请你根据以上数据估计最喜爱“烤肠”的学生人数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的单价比
型芯片的单价比![]() 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买![]() 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买![]() 型芯片的条数相等.
型芯片的条数相等.
(1)求该公司购买的![]() 、
、![]() 型芯片的单价各是多少元?
型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为3的正方形ABCD中,点E是BC边上的点,EC=2,∠AEP=90°,且EP交正方形外角的平分线CP于点P,则PC的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
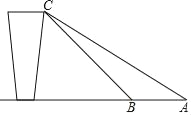
【题目】如图是东方货站传送货物的平面示意图,为了提高安全性,工人师傅打算减小传送带与地面的夹角,由原来的45°改为36°,已知原传送带BC长为4米,求新传送带AC的长及新、原传送带触地点之间AB的长.(结果精确到0.1米)参考数据:sin36°≈0.59,cos36°≈0.1,tan36°≈0.73,![]() 取1.414
取1.414
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)化简函数解析式,当![]() 时,
时,![]() ___________,当
___________,当![]() 时
时![]() ____________;
____________;
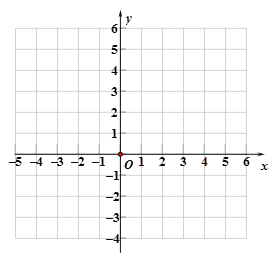
(2)根据(1)中的结果,请在所给坐标系中画出函数![]() 的图象;备用图
的图象;备用图
(3)结合画出的函数图象,解决问题:若关于![]() 的方程
的方程![]() 只有一个实数根,直接写出实数
只有一个实数根,直接写出实数![]() 的取值范围:___________________________.
的取值范围:___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
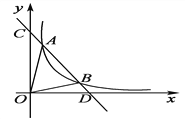
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-![]() <0时x的取值范围;
<0时x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
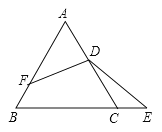
【题目】如图,△ABC是等边三角形,D是AC的中点,点E在BC的延长线上,点F在AB上,![]() .若AB=5,则BE+BF的长度为( )
.若AB=5,则BE+BF的长度为( )
A.7.5B.8C.8.5D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com