
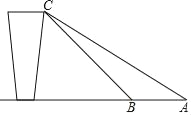
【题目】如图是东方货站传送货物的平面示意图,为了提高安全性,工人师傅打算减小传送带与地面的夹角,由原来的45°改为36°,已知原传送带BC长为4米,求新传送带AC的长及新、原传送带触地点之间AB的长.(结果精确到0.1米)参考数据:sin36°≈0.59,cos36°≈0.1,tan36°≈0.73,![]() 取1.414
取1.414
【答案】新传送带AC的长为4.8m,新、原传送带触地点之间AB的长约为1.0m.
【解析】
根据题意得出:∠A=36°,∠CBD=45°,BC=4,即可得出BD的长,再表示出AD的长,进而求出AB的长.
如图,作CD⊥AB于点D,由题意可得:∠A=36°,∠CBD=45°,BC=4.
在Rt△BCD中,sin∠CBD=![]() ,∴CD=BCsin∠CBD=2
,∴CD=BCsin∠CBD=2![]() .
.
∵∠CBD=45°,∴BD=CD=2![]() .
.
在Rt△ACD中,sinA=![]() ,tanA=
,tanA=![]() ,∴AC=
,∴AC=![]() ≈
≈![]() ≈4.8,AD=
≈4.8,AD=![]() =
=![]() ,∴AB=AD﹣BD=
,∴AB=AD﹣BD=![]() ﹣2
﹣2![]() =
=![]() ﹣2×1.414≈3.87﹣2.83=1.04≈1.0.
﹣2×1.414≈3.87﹣2.83=1.04≈1.0.

答:新传送带AC的长为4.8m,新、原传送带触地点之间AB的长约为1.0m.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙、丙三明射击队员在某次训练中的成绩如下表:
队员 | 成绩(单位:环) | |||||||||
甲 | 6 | 6 | 7 | 7 | 8 | 9 | 9 | 9 | 9 | 10 |
乙 | 6 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 10 |
丙 | 6 | 6 | 6 | 7 | 7 | 8 | 10 | 10 | 10 | 10 |
针对上述成绩,三位教练是这样评价的:
教练![]() :三名队员的水平相当;
:三名队员的水平相当;
教练![]() :三名队员每人都有自己的优势;
:三名队员每人都有自己的优势;
教练![]() :如果从不同的角度分析,教练
:如果从不同的角度分析,教练![]() 和
和![]() 说的都有道理.
说的都有道理.
你同意教练![]() 的观点吗?通过数据分析,说明你的理由.
的观点吗?通过数据分析,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师所留的作业中有这样一个分式的计算题:![]() ,甲、乙两位同学完成的过程分别如下:
,甲、乙两位同学完成的过程分别如下:
甲同学:
![]()
![]() 第一步
第一步
![]() 第二步
第二步
![]() 第三步
第三步
乙同学:
![]()
![]() 第一步
第一步
![]() 第二步
第二步
![]() 第三步
第三步
老师发现这两位同学的解答都有错误:
(1)甲同学的解答从第______步开始出现错误;乙同学的解答从第_____步开始出现错误;
(2)请重新写出完成此题的正确解答过程.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘广告策划人员一名,对甲、乙、丙三名候选人进行三项素质测试,他们的各项测试成绩如下表所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
创新 | 72 | 85 | 67 |
综合知识 | 50 | 74 | 70 |
语言 | 88 | 45 | 67 |
(1)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按5:3:2的比例确定各人的测试成绩,此时谁将被录用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c(b,c是常数)与x轴相交于A,B两点(A在B的左侧),与y轴交于点C.
(1)当A(﹣1,0),C(0,﹣3)时,求抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点.
①当点P关于原点的对称点P′落在直线BC上时,求m的值;
②当点P关于原点的对称点P′落在第一象限内,P′A2取得最小值时,求m的值及这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A是x轴外的一点,若平面内的点B满足:线段AB的长度与点A到x轴的距离相等,则称点B是点A的“等距点”.
(1)若点A的坐标为(0,2),点![]() (2,2),
(2,2),![]() (1,
(1,![]() ),
),![]() (
(![]() ,1)中,点A的“等距点”是_______________;
,1)中,点A的“等距点”是_______________;
(2)若点M(1,2)和点N(1,8)是点A的两个“等距点”,求点A的坐标;
(3)记函数![]() (
(![]() )的图象为
)的图象为![]() ,
,![]() 的半径为2,圆心坐标为
的半径为2,圆心坐标为![]() .若在
.若在![]() 上存在点M,
上存在点M,![]() 上存在点N,满足点N是点M的“等距点”,直接写出t的取值范围.
上存在点N,满足点N是点M的“等距点”,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 是
是![]() 的中点,延长
的中点,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() (如图①).
(如图①).

(1)求证:![]() ≌
≌![]() ;
;
(2)已知点![]() 是
是![]() 的中点,连接
的中点,连接![]() (如图②).
(如图②).
①求证:![]() ≌
≌![]() ;
;
②如图③,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读探索题:
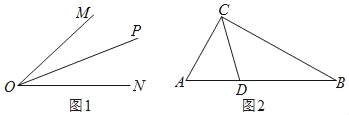
(1)如图1,OP是∠MON的平分线,以O为圆心任意长为半径作弧,分别交射线ON、OM于C、B两点,在射线OP上任取一点A(点O除外),连接AB、AC.求证:△AOB≌△AOC.
(2)请你参考以上方法,解答下列问题:
如图2,在 Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com