
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§ΒψA «x÷αΆβΒΡ“ΜΒψΘ§»τΤΫΟφΡΎΒΡΒψB¬ζΉψΘΚœΏΕΈABΒΡ≥ΛΕ»”κΒψAΒΫx÷αΒΡΨύάκœύΒ»Θ§‘ρ≥ΤΒψB «ΒψAΒΡΓΑΒ»ΨύΒψΓ±Θ°
Θ®1Θ©»τΒψAΒΡΉχ±ξΈΣΘ®0Θ§2Θ©Θ§Βψ![]() Θ®2Θ§2Θ©Θ§
Θ®2Θ§2Θ©Θ§![]() Θ®1Θ§
Θ®1Θ§![]() Θ©Θ§
Θ©Θ§![]() Θ®
Θ®![]() Θ§1Θ©÷–Θ§ΒψAΒΡΓΑΒ»ΨύΒψΓ± «_______________ΘΜ
Θ§1Θ©÷–Θ§ΒψAΒΡΓΑΒ»ΨύΒψΓ± «_______________ΘΜ
Θ®2Θ©»τΒψMΘ®1Θ§2Θ©ΚΆΒψNΘ®1Θ§8Θ© «ΒψAΒΡΝΫΗωΓΑΒ»ΨύΒψΓ±Θ§«σΒψAΒΡΉχ±ξΘΜ
Θ®3Θ©Φ«Κ· ΐ![]() Θ®
Θ®![]() Θ©ΒΡΆΦœσΈΣ
Θ©ΒΡΆΦœσΈΣ![]() Θ§
Θ§![]() ΒΡΑκΨΕΈΣ2Θ§‘≤–ΡΉχ±ξΈΣ
ΒΡΑκΨΕΈΣ2Θ§‘≤–ΡΉχ±ξΈΣ![]() .»τ‘Ύ
.»τ‘Ύ![]() …œ¥φ‘ΎΒψMΘ§
…œ¥φ‘ΎΒψMΘ§![]() …œ¥φ‘ΎΒψNΘ§¬ζΉψΒψN «ΒψMΒΡΓΑΒ»ΨύΒψΓ±Θ§÷±Ϋ”–¥≥ωtΒΡ»Γ÷ΒΖΕΈßΘ°
…œ¥φ‘ΎΒψNΘ§¬ζΉψΒψN «ΒψMΒΡΓΑΒ»ΨύΒψΓ±Θ§÷±Ϋ”–¥≥ωtΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©œξΦϊΫβΈωΘΜΘ®2Θ©Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Μρ
Μρ![]() Θ°Θ®3Θ©
Θ°Θ®3Θ©![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΒ»ΨύΒψΒΡΕ®“εΩ…«σΒψAΒΡΒ»ΨύΒψΒΡΉχ±ξ;
Θ®2Θ©ΗυΨίΒ»ΨύΒψΒΡΕ®“εΩ…«σΒψAΒΡΉχ±ξ;
Θ®3Θ©ΗυΨίΒψN «ΒψMΒΡΓΑΒ»ΨύΒψΓ±Θ§ “Ή÷ΣΒ±ΒψN‘ΎΓ―T…œ‘ΥΕ· ±Θ§ΒψM‘ΎL…œ‘ΥΕ·Θ§”…¥ΥΩ…«σ≥ωtΒΡ»Γ÷ΒΖΕΈßΘ°
Θ®1Θ©![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Θ®2Θ©ΓΏΒψ![]() ΚΆΒψ
ΚΆΒψ![]() «ΒψAΒΡΝΫΗωΓΑΒ»ΨύΒψΓ± Θ§
«ΒψAΒΡΝΫΗωΓΑΒ»ΨύΒψΓ± Θ§
Γύ![]() Θ°
Θ°
ΓύΒψA‘ΎœΏΕΈMNΒΡ¥Ι÷±ΤΫΖ÷œΏ…œΘ°
…η![]() ”κΤδ¥Ι÷±ΤΫΖ÷œΏΫΜ”ΎΒψ
”κΤδ¥Ι÷±ΤΫΖ÷œΏΫΜ”ΎΒψ![]() Θ§
Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§![]() Θ°
Θ°
Γύ![]() .
.
Γύ![]() Θ°
Θ°
ΓύΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Μρ
Μρ![]() Θ°
Θ°
Θ®3Θ©![]() Θ°
Θ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
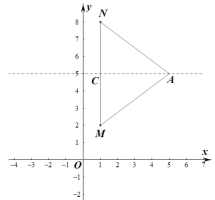
ΓΨΧβΡΩΓΩ‘ΎΓςABC÷–Θ§ABΓΔAC±ΏΒΡ¥Ι÷±ΤΫΖ÷œΏΖ÷±πΫΜBC±Ώ”ΎΒψMΓΔN
Θ®1Θ©»γΆΦΔΌΘ§»τΓœBACΘΫ110ΓψΘ§‘ρΓœMANΘΫΓΓ ΓΓΓψΘ§»τΓςAMNΒΡ÷ή≥ΛΈΣ9Θ§‘ρBCΘΫΓΓ
Θ®2Θ©»γΆΦΔΎΘ§»τΓœBACΘΫ135ΓψΘ§«σ÷ΛΘΚBM2+CN2ΘΫMN2ΘΜ
Θ®3Θ©»γΆΦΔέΘ§ΓœABCΒΡΤΫΖ÷œΏBPΚΆAC±ΏΒΡ¥Ι÷±ΤΫΖ÷œΏœύΫΜ”ΎΒψPΘ§ΙΐΒψPΉςPH¥Ι÷±BAΒΡ―”≥ΛœΏ”ΎΒψHΘ°»τABΘΫ5Θ§CBΘΫ12Θ§«σAHΒΡ≥Λ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
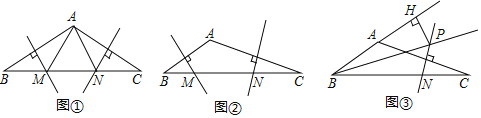
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§Βψ
Θ§Βψ![]() ―Ί±Ώ
―Ί±Ώ![]() ¥”Βψ
¥”Βψ![]() œρΒψ
œρΒψ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·ΘΜΆ§ ±Θ§Βψ
ΒΡΥΌΕ»“ΤΕ·ΘΜΆ§ ±Θ§Βψ![]() ¥”Βψ
¥”Βψ![]() ―Ί±Ώ
―Ί±Ώ![]() œρΒψ
œρΒψ![]() “‘
“‘![]() ΒΡΥΌΕ»“ΤΕ·Θ§…ηΒψ
ΒΡΥΌΕ»“ΤΕ·Θ§…ηΒψ![]() ΓΔ
ΓΔ![]() “ΤΕ·ΒΡ ±ΦδΈΣ
“ΤΕ·ΒΡ ±ΦδΈΣ![]() Θ°Έ ΘΚ
Θ°Έ ΘΚ
![]() Β±
Β±![]() ΈΣΚΈ÷Β ±
ΈΣΚΈ÷Β ±![]() ΒΡΟφΜΐΒ»”Ύ
ΒΡΟφΜΐΒ»”Ύ![]() ΘΩ
ΘΩ
![]() Β±
Β±![]() ΈΣΚΈ÷Β ±
ΈΣΚΈ÷Β ±![]() «÷±Ϋ«»ΐΫ«–ΈΘΩ
«÷±Ϋ«»ΐΫ«–ΈΘΩ
![]() «Ζώ¥φ‘Ύ
«Ζώ¥φ‘Ύ![]() ΒΡ÷ΒΘ§ Ι
ΒΡ÷ΒΘ§ Ι![]() ΒΡΟφΜΐΉν–ΓΘ§»τ¥φ‘ΎΘ§«σ¥Υ ±
ΒΡΟφΜΐΉν–ΓΘ§»τ¥φ‘ΎΘ§«σ¥Υ ±![]() ΒΡ÷ΒΦΑ¥Υ ±ΒΡΟφΜΐΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡ÷ΒΦΑ¥Υ ±ΒΡΟφΜΐΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
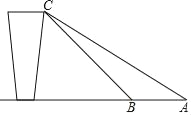
ΓΨΧβΡΩΓΩ»γΆΦ «ΕΪΖΫΜθ’Ψ¥ΪΥΆΜθΈοΒΡΤΫΟφ Ψ“βΆΦΘ§ΈΣΝΥΧαΗΏΑ≤»Ϊ–‘Θ§ΙΛ»Υ ΠΗΒ¥ρΥψΦθ–Γ¥ΪΥΆ¥χ”κΒΊΟφΒΡΦ–Ϋ«Θ§”…‘≠ά¥ΒΡ45ΓψΗΡΈΣ36ΓψΘ§“―÷Σ‘≠¥ΪΥΆ¥χBC≥ΛΈΣ4ΟΉΘ§«σ–¬¥ΪΥΆ¥χACΒΡ≥ΛΦΑ–¬ΓΔ‘≠¥ΪΥΆ¥χ¥ΞΒΊΒψ÷°ΦδABΒΡ≥ΛΘ°Θ®ΫαΙϊΨΪ»ΖΒΫ0.1ΟΉΘ©≤ΈΩΦ ΐΨίΘΚsin36ΓψΓ÷0.59Θ§cos36ΓψΓ÷0.1Θ§tan36ΓψΓ÷0.73Θ§![]() »Γ1.414
»Γ1.414
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
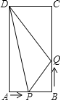
ΓΨΧβΡΩΓΩœ¬Οφ «–ΓΕ≠…ηΦΤΒΡΓΑΉς“―÷Σ‘≤ΒΡΡΎΫ”’ΐ»ΐΫ«–ΈΓ±ΒΡ≥ΏΙφΉςΆΦΙΐ≥Χ.
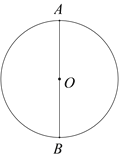
“―÷ΣΘΚΓ―OΘ°
«σΉςΘΚΓ―OΒΡΡΎΫ”’ΐ»ΐΫ«–ΈΘ°
ΉςΖ®ΘΚ»γΆΦΘ§
ΔΌΉς÷±ΨΕABΘΜ
ΔΎ“‘BΈΣ‘≤–ΡΘ§OBΈΣΑκΨΕΉςΜΓΘ§”κΓ―OΫΜ”ΎCΘ§DΝΫΒψΘΜ
ΔέΝ§Ϋ”ACΘ§ADΘ§CDΘ°
Υυ“‘ΓςACDΨΆ «Υυ«σΒΡ»ΐΫ«–ΈΘ°
ΗυΨί–ΓΕ≠…ηΦΤΒΡ≥ΏΙφΉςΆΦΙΐ≥ΧΘ§
Θ®1Θ© Ι”Ο÷±≥ΏΚΆ‘≤ΙφΘ§≤Ι»ΪΆΦ–ΈΘΜΘ®±ΘΝτΉςΆΦΚέΦΘΘ©
Θ®2Θ©Άξ≥…œ¬ΟφΒΡ÷ΛΟςΘΚ
÷ΛΟςΘΚ‘ΎΓ―O÷–Θ§Ν§Ϋ”OCΘ§ODΘ§BCΘ§BDΘ§
ÿOC=OB=BCȧ
ΓύΓςOBCΈΣΒ»±Ώ»ΐΫ«–ΈΘ®_______________Θ©Θ®ΧνΆΤάμΒΡ“άΨίΘ©Θ°
ΓύΓœBOC=60ΓψΘ°
ΓύΓœAOC=180Γψ-ΓœBOC=120ΓψΘ°
Ά§άμΓœAOD=120ΓψΘ§
ΓύΓœCOD=ΓœAOC=ΓœAOD=120ΓψΘ°
ΓύAC=CD=ADΘ®_______________Θ©Θ®ΧνΆΤάμΒΡ“άΨίΘ©Θ°
ΓύΓςACD «Β»±Ώ»ΐΫ«–ΈΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
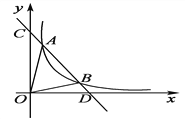
ΓΨΧβΡΩΓΩ»γΆΦΘ§“Μ¥ΈΚ· ΐy=kx+b”κΖ¥±»άΐΚ· ΐy=![]() Θ®xΘΨ0Θ©ΒΡΆΦœσΫΜ”ΎAΘ®mΘ§6Θ©Θ§BΘ®3Θ§nΘ©ΝΫΒψ.
Θ®xΘΨ0Θ©ΒΡΆΦœσΫΜ”ΎAΘ®mΘ§6Θ©Θ§BΘ®3Θ§nΘ©ΝΫΒψ.
Θ®1Θ©«σ“Μ¥ΈΚ· ΐΒΡΫβΈω ΫΘΜ
(2)ΗυΨίΆΦœσ÷±Ϋ”–¥≥ωkx+b-![]() ΘΦ0 ±xΒΡ»Γ÷ΒΖΕΈß;
ΘΦ0 ±xΒΡ»Γ÷ΒΖΕΈß;
(3)«σΓςAOBΒΡΟφΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒ±Ρψ’Ψ‘Ύ≤©ΈοΙίΒΡ’ΙάάΧϋ÷– ±Θ§Ρψ÷ΣΒά’Ψ‘ΎΚΈ¥ΠΙέ…ΆΉνάμœκ¬πΘΩ»γΆΦΘ§…η«Ϋ±Ύ…œΒΡ’ΙΤΖΉνΗΏΒψPΨύΒΊΟφ2.5ΟΉΘ§ΉνΒΆΒψQΨύΒΊΟφ2ΟΉΘ§Ιέ…Ά’ΏΒΡ―έΨΠFΨύΒΊΟφ1.6ΟΉΘ§Β± ”Ϋ«ΓœPEQΉν¥σ ±Θ§’Ψ‘Ύ¥Υ¥ΠΙέ…ΆΉνάμœκΘ§‘ρ¥Υ ±EΒΫ«Ϋ±ΎΒΡΨύάκΈΣΘ® Θ©ΟΉΘ°

A. 1 B. 0.6 C. 0.5 D. 0.4
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΙΊ”ΎxΒΡΚ· ΐy=Θ®a+2Θ©x2©¹Θ®2a©¹1Θ©x+a©¹2ΒΡΆΦœσ”κΉχ±ξ÷α”–ΝΫΗωΫΜΒψΘ§‘ρaΒΡ÷ΒΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
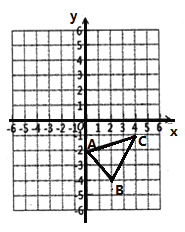
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§
Θ®1Θ©Ής≥ω![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ÷αΕ‘≥ΤΒΡ
÷αΕ‘≥ΤΒΡ![]() Θ§≤Δ–¥≥ω
Θ§≤Δ–¥≥ω![]() »ΐΗωΕΞΒψΒΡΉχ±ξΘΜ
»ΐΗωΕΞΒψΒΡΉχ±ξΘΜ
Θ®2Θ©«κΦΤΥψ![]() ΒΡΟφΜΐΘΜ
ΒΡΟφΜΐΘΜ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com