
【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N
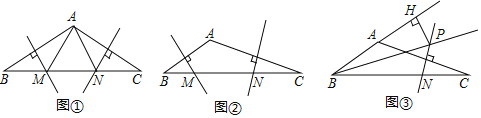
(1)如图①,若∠BAC=110°,则∠MAN= °,若△AMN的周长为9,则BC=
(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2;
(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=5,CB=12,求AH的长
【答案】(1)40;9;(2)见详解;(3)3.5
【解析】
(1)根据线段垂直平分线的性质得到AM=BM,NA=NC,根据等腰三角形的性质得到BAM=∠B,∠NAC=∠C,结合图形计算即可;
(2)连接AM、AN,仿照(1)的作法得到∠MAN=90°,根据勾股定理证明结论;
(3)连接AP、CP,过点P作PE⊥BC于点E,根据线段垂直平分线的性质得到AP=CP,根据角平分线的性质得到PH=PE,证明Rt△APH≌Rt△CPE得到AH=CE,证明△BPH≌△BPE,得到BH=BE,结合图形计算即可.
解:(1)∵∠BAC=110°,
∴∠B+∠C=180°﹣110°=70°,
∵AB边的垂直平分线交BC边于点M,
∴AM=BM,
∴∠BAM=∠B,
同理:NA=NC,
∴∠NAC=∠C,
∴∠MAN=110°﹣(∠BAM+∠NAC)=40°,
∵△AMN的周长为9,
∴MA+MN+NA=9,
∴BC=MB+MN+NC=MA+MN+NA=9,
故答案为:40;9;
(2)如图②,连接AM、AN,
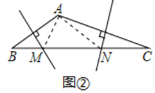
∵∠BAC=135°,
∴∠B+∠C=45°,
∵点M在AB的垂直平分线上,
∴AM=BM,
∴∠BAM=∠B,
同理AN=CN,∠CAN=∠C,
∴∠BAM+∠CAN=45°,
∴∠MAN=∠BAC﹣(∠BAM+∠CAN)=90°,
∴AM2+AN2=MN2,
∴BM2+CN2=MN2;
(3)如图③,连接AP、CP,过点P作PE⊥BC于点E,
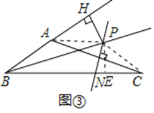
∵BP平分∠ABC,PH⊥BA,PE⊥BC,
∴PH=PE,
∵点P在AC的垂直平分线上,
∴AP=CP,
在Rt△APH和Rt△CPE中,
![]() ,
,
∴Rt△APH≌Rt△CPE(HL),
∴AH=CE,
在△BPH和△BPE中,
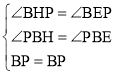 ,
,
∴△BPH≌△BPE(AAS)
∴BH=BE,
∴BC=BE+CE=BH+CE=AB+2AH,
∴AH=(BC﹣AB)÷2=3.5.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】从某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分四个等级,将调查结果绘制成如下的不完整的条形统计图和扇形统计图.根据图中信息.
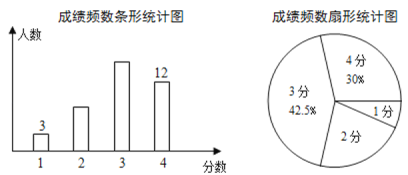
(1)求共抽取多少名学生;
(2)求抽取的所有学生成绩的众数,中位数;
(3)求抽取的所有学生成绩的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交于点H,连接BD、FH.
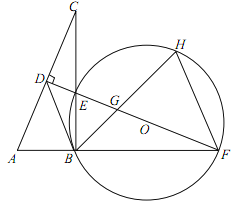
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HGHB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三明射击队员在某次训练中的成绩如下表:
队员 | 成绩(单位:环) | |||||||||
甲 | 6 | 6 | 7 | 7 | 8 | 9 | 9 | 9 | 9 | 10 |
乙 | 6 | 7 | 7 | 8 | 8 | 8 | 8 | 9 | 9 | 10 |
丙 | 6 | 6 | 6 | 7 | 7 | 8 | 10 | 10 | 10 | 10 |
针对上述成绩,三位教练是这样评价的:
教练![]() :三名队员的水平相当;
:三名队员的水平相当;
教练![]() :三名队员每人都有自己的优势;
:三名队员每人都有自己的优势;
教练![]() :如果从不同的角度分析,教练
:如果从不同的角度分析,教练![]() 和
和![]() 说的都有道理.
说的都有道理.
你同意教练![]() 的观点吗?通过数据分析,说明你的理由.
的观点吗?通过数据分析,说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A为y轴正半轴上一点,过点A作x轴的平行线,交函数![]() 的图象于B点,交函数
的图象于B点,交函数![]() 的图象于C,过C作y轴和平行线交BO的延长线于D.
的图象于C,过C作y轴和平行线交BO的延长线于D.
(1)如果点A的坐标为(0,2),求线段AB与线段CA的长度之比;
(2)如果点A的坐标为(0,a),求线段AB与线段CA的长度之比;
(3)在(1)条件下,四边形AODC的面积为多少?
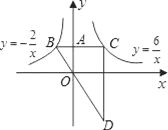
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定水费实行两级收费制度.若每月用水量不超过10吨(含10吨),则每吨按优惠价m元收费;若每月用水量超过10吨,则超过部分每吨按市场价![]() 元收费,小明家3月份用水20吨,交水费50元;4月份用水18吨,交水费44元.
元收费,小明家3月份用水20吨,交水费50元;4月份用水18吨,交水费44元.
(1)求每吨水的优惠价和市场价分别是多少?
(2)设每月用水量为![]() 吨,应交水费为
吨,应交水费为![]() 元,请写出
元,请写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y1=﹣2x+b的图象交x轴于点A、与正比例函数y2=2x的图象交于点M(m,m+2),
(1)求点M坐标;
(2)求b值;
(3)点O为坐标原点,试确定△AOM的形状,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师所留的作业中有这样一个分式的计算题:![]() ,甲、乙两位同学完成的过程分别如下:
,甲、乙两位同学完成的过程分别如下:
甲同学:
![]()
![]() 第一步
第一步
![]() 第二步
第二步
![]() 第三步
第三步
乙同学:
![]()
![]() 第一步
第一步
![]() 第二步
第二步
![]() 第三步
第三步
老师发现这两位同学的解答都有错误:
(1)甲同学的解答从第______步开始出现错误;乙同学的解答从第_____步开始出现错误;
(2)请重新写出完成此题的正确解答过程.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A是x轴外的一点,若平面内的点B满足:线段AB的长度与点A到x轴的距离相等,则称点B是点A的“等距点”.
(1)若点A的坐标为(0,2),点![]() (2,2),
(2,2),![]() (1,
(1,![]() ),
),![]() (
(![]() ,1)中,点A的“等距点”是_______________;
,1)中,点A的“等距点”是_______________;
(2)若点M(1,2)和点N(1,8)是点A的两个“等距点”,求点A的坐标;
(3)记函数![]() (
(![]() )的图象为
)的图象为![]() ,
,![]() 的半径为2,圆心坐标为
的半径为2,圆心坐标为![]() .若在
.若在![]() 上存在点M,
上存在点M,![]() 上存在点N,满足点N是点M的“等距点”,直接写出t的取值范围.
上存在点N,满足点N是点M的“等距点”,直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com