
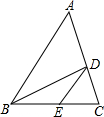
 如图,△ABC中,CE:EB=2:3,DE∥AB,若△ABC的面积为25,则△BDE的面积为6.
如图,△ABC中,CE:EB=2:3,DE∥AB,若△ABC的面积为25,则△BDE的面积为6. 分析 由DE∥AB,CE:CB=2:5,可知S△CDE:S△ABC=4:25,因为△ABC的面积为25,所以△CDE的面积为4,由CE:EB=2:3,可知S△BDE:S△CDE=3:2,所以△BDE的面积为$\frac{3}{2}$×4=6.
解答 解:∵DE∥AB,
∴△CDE∽△CAB,
∵CE:EB=2:3,
∴CE:CB=2:5,
∴S△CDE:S△ABC=4:25,
∵S△ABC=25,
∴S△CDE=4,
∵CE:EB=2:3,
∴S△BDE:S△CDE=3:2,
∴S△BDE=6.
点评 本题主要考查了相似三角形的性质和面积变换,相似三角形的面积比等于相似比的平方,等高的三角形面积比等于底的比,等底的三角形面积比等于高的比.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
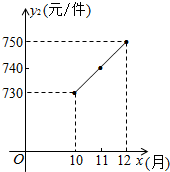 某企业为重庆计算机产业基地提供电脑配件,受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
某企业为重庆计算机产业基地提供电脑配件,受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
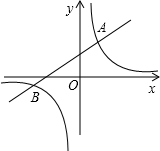 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com