
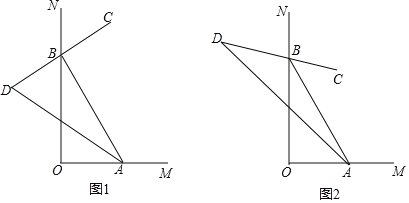
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.
(1)若AD=3![]() ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE=![]() EF;
EF;
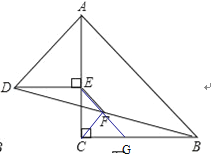
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.

【答案】(1)EF =2.5;(2)证明见解析;(3)(1)中的结论仍然成立.理由见解析.
【解析】试题分析:(1)等腰直角三角形的斜边长是直角边的![]() 倍,得到DE=3由于BE=4,利用勾股定理,得BD=5,再利用直角三角形斜边上的中线是斜边的一半,得以解决;
倍,得到DE=3由于BE=4,利用勾股定理,得BD=5,再利用直角三角形斜边上的中线是斜边的一半,得以解决;
(2)连接CF,需要证明![]() 是等腰直角三角形,根据四点共圆,得到点F是四边形DCBE的外接圆,且F是圆心,根据同弧所对的圆心角是圆周角的2倍,得
是等腰直角三角形,根据四点共圆,得到点F是四边形DCBE的外接圆,且F是圆心,根据同弧所对的圆心角是圆周角的2倍,得![]() 从而
从而![]() ,再根据直角三角形斜边上的中线是斜边的一半,得
,再根据直角三角形斜边上的中线是斜边的一半,得![]() ,得证
,得证![]() 是等腰直角三角形,结论得证;
是等腰直角三角形,结论得证;
(3)连接CF,延长EF交CB于点G,利用ASA证明△EDF≌△GBF,得出EF=GF,BG=DE=AE,进而证明CE=CG,得出△CEF为等腰直角三角形,利用三线合一证明![]() 结论得证。
结论得证。
试题解析:
(1)∵∠AED=90°,AE=DE,AD=3![]() ,
,
∴AE=DE=3,
在Rt△BDE中,
∵DE=3,BE=4,
∴BD=5,
又∵F是线段BD的中点,
∴EF=![]() BD=2.5;
BD=2.5;
(2)连接CF,线段CE与FE之间的数量关系是CE=![]() FE;
FE;
∵∠AED=∠ACB=90°
∴B、C、D、E四点共圆
且BD是该圆的直径,
∵点F是BD的中点,
∴点F是圆心,
∴EF=CF=FD=FB,
∴∠FCB=∠FBC,∠ECF=∠CEF,
由圆周角定理得:∠DCE=∠DBE,
∴∠FCB+∠DCE=∠FBC+∠DBE=45°
∴∠ECF=45°=∠CEF,
∴△CEF是等腰直角三角形,
∴CE=![]() EF.
EF.
(3)(1)中的结论仍然成立.
如图,连接CF,延长EF交CB于点G,
∵∠ACB=∠AED=90°,
∴DE∥BC,
∴∠EDF=∠GBF,
在△EDF和△GBF中,
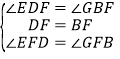 ,
,
∴△EDF≌△GBF,
∴EF=GF,BG=DE=AE,
∵AC=BC,
∴CE=CG,
∴∠EFC=90°,CF=EF,
∴△CEF为等腰直角三角形,
∴∠CEF=45°,
∴CE=![]() FE;
FE;


科目:初中数学 来源: 题型:
【题目】如图1,已知点A(-2,0).点D在y轴上,连接AD并将它沿x轴向右平移至BC的位置,且点B坐标为(4,0),连接CD,OD=![]() AB.
AB.
(1)线段CD的长为 ,点C的坐标为 ;
(2)如图2,若点M从点B出发,以1个单位长度/秒的速度沿着x轴向左运动,同时点N从原点O出发,以相同的速度沿折线OD→DC运动(当N到达点C时,两点均停止运动).假设运动时间为t秒.
①t为何值时,MN∥y轴;
②求t为何值时,S△BCM=2S△ADN.

查看答案和解析>>
科目:初中数学 来源: 题型:
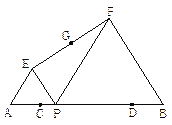
【题目】如图:已知AB=10,点C、D在线段AB上且AC=DB=2; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD.
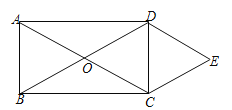
(1)求证:四边形OCED是菱形;
(2)若AB=3,AD=4,求四边形OCED的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课前预习是学习的重要环节,为了了解所教班级学生完成课前预习的具体情况,某班主任对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类:A.优秀,B.良好,C.一般,D.较差,并将调查结果绘制成以下两幅不完整的统计图.
(1)本次调查的样本容量是 ;其中A类女生有 名,D类学生有 名;
(2)将条形统计图和扇形统计图补充完整;
(3)若从被调查的A类和D类学生中各随机选取一位学生进行“一帮一”辅导学习,即A类学生辅导D类学生,请用列表法或画树状图的方法求出所选两位同学中恰好是一位女同学辅导一位男同学的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形![]() 外取一点
外取一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .过点
.过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .若
.若![]() ,
,![]() .下列结论:①
.下列结论:①![]() ;②点
;②点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;其中正确结论的序号是( )
;其中正确结论的序号是( )

A.①③④B.①②⑤C.③④⑤D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=ɑ(0°<ɑ<180°),点A.B分别在OM、ON上运动(不与点O重合).
(1)如图1,∠MON=90°,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交与点D.
①若∠BAO=60°,则∠D=___.
②猜想:∠D的度数是否随A,B的移动发生变化?并说明理由。
(2)如图2,∠MON=α(0°<α<180°)”,∠ABC=![]() ∠ABN,∠BAD=
∠ABN,∠BAD=![]() ∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 | 100 | 1 |
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com