
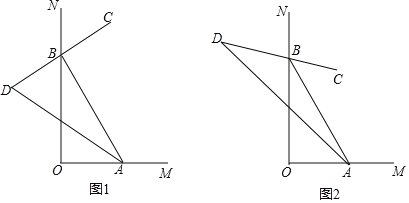
【题目】如图,∠MON=ɑ(0°<ɑ<180°),点A.B分别在OM、ON上运动(不与点O重合).
(1)如图1,∠MON=90°,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交与点D.
①若∠BAO=60°,则∠D=___.
②猜想:∠D的度数是否随A,B的移动发生变化?并说明理由。
(2)如图2,∠MON=α(0°<α<180°)”,∠ABC=![]() ∠ABN,∠BAD=
∠ABN,∠BAD=![]() ∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
【答案】①45;②∠D的度数不随A,B的移动发生变化; ![]()
【解析】
(1)①根据邻补角的定义及角平分线定义求出∠BAD =30°,∠ABC =75°,然后根据三角形外角的性质可求出∠D;②设∠BAO=x,步骤同①可得∠D的度数不随A,B的移动发生变化;
(2)根据三角形外角的性质可得∠D=∠ABC-∠BAD,然后将∠ABC=![]() ∠ABN,∠BAD=
∠ABN,∠BAD=![]() ∠BAO代入化简,即可得出结果.
∠BAO代入化简,即可得出结果.
解:(1)①∵∠MON=90°,∠BAO=60°,
∴∠ABO=30°,∠BAD=![]() ∠BAO =30°
∠BAO =30°
∴∠ABN=150°,
∴∠ABC=![]() ∠ABN=75°,
∠ABN=75°,
∴∠D=∠ABC-∠BAD=45°;
②∠D的度数不随A,B的移动发生变化;
理由:设∠BAO=x,
∴∠ABO=90°-x,∠BAD=![]() ∠BAO=
∠BAO=![]() ,
,
∴∠ABN=180°-(90°-x)=90°+x,
∴∠ABC=![]() ∠ABN=45°+
∠ABN=45°+![]() ,
,
∴∠D=∠ABC-∠BAD=45°+![]() -
-![]() =45°,
=45°,
∴∠D的度数不随A,B的移动发生变化;
(2)∵∠MON=α,∠ABC=![]() ∠ABN,∠BAD=
∠ABN,∠BAD=![]() ∠BAO,
∠BAO,
∴∠D=∠ABC-∠BAD=![]() ∠ABN-
∠ABN-![]() ∠BAO=
∠BAO=![]() (∠ABN-∠BAO)=
(∠ABN-∠BAO)=![]() ∠MON=
∠MON=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的中线,过
边上的中线,过![]() 作
作![]() ,垂足为
,垂足为![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,则下列结论正确的是______.(请填写序号)
,则下列结论正确的是______.(请填写序号)
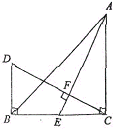
①若![]() ,则
,则![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ;⑥连接
;⑥连接![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
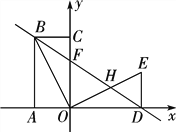
【题目】如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标(-2,4)△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H.
(1) 求直线BD的解析式;
(2) 求△BCF的面积;
(3) 点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上,F是线段BD的中点,连接CE、FE.
(1)若AD=3![]() ,BE=4,求EF的长;
,BE=4,求EF的长;
(2)求证:CE=![]() EF;
EF;
(3)将图1中的△AED绕点A顺时针旋转,使AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次数学兴趣小组活动中,同学们做了一个找朋友的游戏:有六个同学A、B、C、D、E、F分别藏在六张大纸牌的后面,如图,A、B、C、D、E、F所持的纸牌的前面分别写有六个算式:66;63+63;(63)3;(2×62)×(3×63);(22×32)3;(64)3÷62.游戏规定:所持算式的值相等的两个人是朋友.如果现在由同学A来找他的朋友,他可以找谁呢?说说你的看法.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D在△ABC的边BC上,DC=2BD,连接AD与△ABC的中线BE交于点F,连接CF,若△ABC的面积为24,则△AEF的面积为( )

A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据: ![]() ≈1.414,、
≈1.414,、![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在正方形ABCD中.
(1)如图1,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,试判断AE与BF的数量关系,并说明理由;
(2)如图2,点E、F、G、H分别在边BC、CD、DA、AB上,EG、FH相交于点O,∠GOH=90°,且EG=7,求FH的长;
(3)如图3,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,若AB=5,图中阴影部分的面积与正方形的面积之比为4:5,求△ABO的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com