
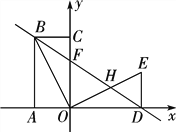
【题目】如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标(-2,4)△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H.
(1) 求直线BD的解析式;
(2) 求△BCF的面积;
(3) 点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)y=-![]() x+
x+![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在, ![]() 或
或![]() 或
或![]()
【解析】试题分析:(1)由B点坐标(-2,4),可求得B、D的坐标,利用待定系数法可求得直线BD的解析式;
(2)可求得E点坐标,求出直线OE的解析式,联立直线BD、OE解析式可求得H点的横坐标,可求得△OFH的面积;
(3)当△MFD为直角三角形时,可找到满足条件的点N,分∠MFD=90°、∠MDF=90°和∠FMD=90°三种情况,分别求得M点的坐标,可分别求得矩形对角线的交点坐标,再利用中点坐标公式可求得N点坐标.
试题解析:(1)B点坐标(-2,4),
∴BC=2,OC=4,
∵△ODE是△OCB绕点O顺时针旋转90°得到的,
∴OD=OC=4,DE=BC=2,
∴D(4,0),
设直线BD解析式为y=kx+b,
把B、D坐标代入可得![]() ,解得
,解得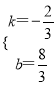 ,
,
∴直线BD的解析式为y=![]() ;
;
(2)由(1)可知E(4,2),
设直线OE解析式为y=mx,
把E点坐标代入可求得m=![]() ,
,
∴直线OE解析式为y=![]() x,
x,
令-![]() =
=![]() x,解得x=
x,解得x=![]() ,
,
∴H点到y轴的距离为![]() ,
,
又由(1)可得F(0, ![]() ),
),
∴OF=![]() ,
,
∴S△OFH=![]() ×
×![]() =
=![]() ;
;
(3)∵以点D、F、M、N为顶点的四边形是矩形,
∴△DFM为直角三角形,
①当∠MFD=90°时,则M只能在x轴上,连接FN交MD于点G,如图1,
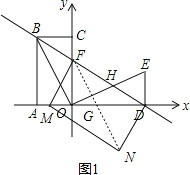
由(2)可知OF=![]() ,OD=4,
,OD=4,
则有△MOF∽△FOD,
∴![]() ,即
,即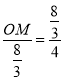 ,解得OM=
,解得OM=![]() ,
,
∴M(-![]() ,0),且D(4,0),
,0),且D(4,0),
∴G(![]() ,0),
,0),
设N点坐标为(x,y),则![]() ,
, 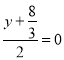 ,
,
解得x=![]() ,y=-
,y=-![]() ,此时N点坐标为(
,此时N点坐标为(![]() ,-
,-![]() );
);
②当∠MDF=90°时,则M只能在y轴上,连接DN交MF于点G,如图2,
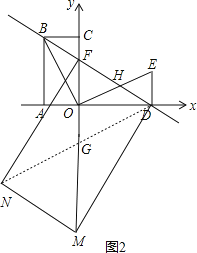
则有△FOD∽△DOM,
∴![]() ,即
,即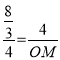 ,解得OM=6,
,解得OM=6,
∴M(0,-6),且F(0, ![]() ),
),
∴MG=![]() MF=
MF=![]() ,则OG=OM-MG=6-
,则OG=OM-MG=6-![]() =
=![]() ,
,
∴G(0,-![]() ),
),
设N点坐标为(x,y),则![]() ,
,![]() ,
,
解得x=-4,y=-![]() ,此时N(-4,-
,此时N(-4,-![]() );
);
③当∠FMD=90°时,则可知M点为O点,如图3,
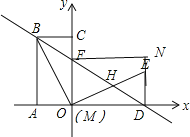
∵四边形MFND为矩形,
∴NF=OD=4,ND=OF=![]() ,
,
可求得N(4, ![]() );
);
综上可知存在满足条件的N点,其坐标为(![]() ,
, ![]() )或(-4,-
)或(-4,-![]() )或(4,
)或(4, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )

A. 4 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°.
(1) 求∠DAC的度数.
(2) 求证:△ACD是等腰三角形.
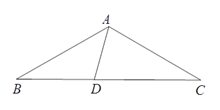
查看答案和解析>>
科目:初中数学 来源: 题型:
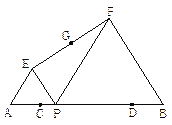
【题目】如图:已知AB=10,点C、D在线段AB上且AC=DB=2; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
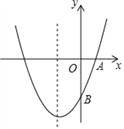
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且经A(1,0)、
B(0,﹣3)两点.(1)求抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上,是否存在点M,使它到点A的距离与到点B的距离之和最小,如果存在求出点M的坐标,如果不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD.
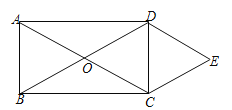
(1)求证:四边形OCED是菱形;
(2)若AB=3,AD=4,求四边形OCED的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课前预习是学习的重要环节,为了了解所教班级学生完成课前预习的具体情况,某班主任对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类:A.优秀,B.良好,C.一般,D.较差,并将调查结果绘制成以下两幅不完整的统计图.
(1)本次调查的样本容量是 ;其中A类女生有 名,D类学生有 名;
(2)将条形统计图和扇形统计图补充完整;
(3)若从被调查的A类和D类学生中各随机选取一位学生进行“一帮一”辅导学习,即A类学生辅导D类学生,请用列表法或画树状图的方法求出所选两位同学中恰好是一位女同学辅导一位男同学的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
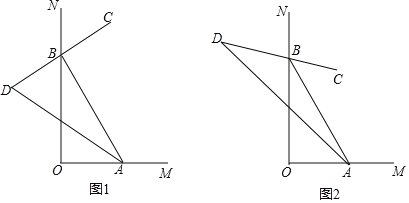
【题目】如图,∠MON=ɑ(0°<ɑ<180°),点A.B分别在OM、ON上运动(不与点O重合).
(1)如图1,∠MON=90°,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交与点D.
①若∠BAO=60°,则∠D=___.
②猜想:∠D的度数是否随A,B的移动发生变化?并说明理由。
(2)如图2,∠MON=α(0°<α<180°)”,∠ABC=![]() ∠ABN,∠BAD=
∠ABN,∠BAD=![]() ∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D、E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,CD=2,则DF的长为( )
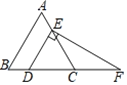
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com