练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在等边三角形ABC中，点D、E分别在边BC，AC上，DE∥AB，过点E作EF⊥DE，交BC的延长线于点F，CD=2，则DF的长为(　　)

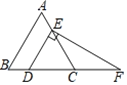
    A.2B.3C.4D.5

    【答案】C

    【解析】

    根据平行线的性质可得∠EDC=∠B=60°，且∠ECD=60°，可知△EDC是等边三角形，已知EF⊥DE，∠DEF=90°，可得∠F=30°，再根据含30°角的直角三角形的性质即可求解．

    ∵△ABC是等边三角形，
    ∴∠B=60°

    ∵DE∥AB，

    ∴∠EDC=∠B=60°

    ∵EF⊥DE，

    ∴∠DEF=90°

    ∴∠F=30°

    ∵∠ACB=∠EDC=60°

    ∴△DEC是等边三角形

    ∴ED=DC=2

    ∵∠DEF=90°，∠F=30°

    ∴DF=2DE=4

    故答案为：4

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

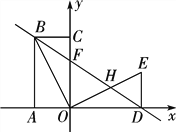
    【题目】如图，四边形OABC是矩形，点A、C在坐标轴上，B点坐标（-2,4）△ODE是△OCB绕点O顺时针旋转90°得到的，点D在x轴上，直线BD交y轴于点F，交OE于点H.

    (1) 求直线BD的解析式；

    (2) 求△BCF的面积；

    (3) 点M在坐标轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请求出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80 m，DE=10 m，求障碍物B，C两点间的距离．(结果精确到0.1 m)（参考数据： ≈1.414，、≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 在正方形ABCD中．

    （1）如图1，点E、F分别在BC、CD上，AE、BF相交于点O，∠AOB=90°，试判断AE与BF的数量关系，并说明理由；

    （2）如图2，点E、F、G、H分别在边BC、CD、DA、AB上，EG、FH相交于点O，∠GOH=90°，且EG=7，求FH的长；

    （3）如图3，点E、F分别在BC、CD上，AE、BF相交于点O，∠AOB=90°，若AB=5，图中阴影部分的面积与正方形的面积之比为4：5，求△ABO的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小华剪了两条宽为3的纸条，交叉叠放在一起，且它们较小的交角为60°，则它们重叠部分的面积为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC是等腰直角三角形，∠ACB=90°，AB=4，点D是AB的中点，动点P、Q同时从点D出发（点P、Q不与点D重合），点P沿D→A以1cm/s的速度向中点A运动．点Q沿D→B→D以2cm/s的速度运动．回到点D停止．以PQ为边在AB上方作正方形PQMN，设正方形PQMN与△ABC重叠部分的面积为S（cm2），点P运动的时间为t（s）．

    （1）当点N在边AC上时，求t的值．

    （2）用含t的代数式表示PQ的长．

    （3）当点Q沿D→B运动，正方形PQMN与△ABC重叠部分图形是五边形时，求S与t之间的函数关系式．

    （4）直接写出正方形PQMN与△ABC重叠部分图形是轴对称图形时t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】认真阅读下面的材料，完成有关问题．

    材料：在学习绝对值时，老师教过我们绝对值的几何含义，如表示、在数轴上对应的两点之间的距离；，所以表示、在数轴上对应的两点之间的距离；，所以表示在数轴上对应的点到原点的距离．

    一般地，点、点在数轴上分别表示有理数、，那么点、点之间的距离可表示为．

    （1）点、、在数轴上分别表示有理数、、，那么点到点的距离与点到点的距离之和可表示为__________（用含绝对值的式子表示）．

    （2）利用数轴探究：

    ①满足的的取值范围是__________．

    ②满足的的所有值是__________．

    ③设，当的值取在不小于且不大于的范围时，的值是不变的，而且是的最小值，这个最小值是_____．

    （3）拓展：

    ①的最小值为__________．

    ②的最小值为__________．

    ③的最小值为__________，此时的取值范围为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品共50件，已知生产一件A种产品用甲种原料9千克，乙种原料3千克，可获利700元；生产一件B种产品用甲种原料4千克，乙种原料10千克，可获利1200元．

    （1）按要求安排A、B两种产品的生产件数，有哪几种方案？请你设计出来；

    （2）设生产A、B两种产品总利润为y元，其中一种产品生产件数为x件，试写出y与x之间的函数关系式，并利用函数的性质说明那种方案获利最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝－x2－2x＋3的图象与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C，点D为抛物线的顶点．

    (1)求点A、B、C的坐标；

    (2)点M为线段AB上一点(点M不与点A、B重合)，过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；

    (3)在(2)的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作

    y轴的平行线，与直线AC交于点G(点G在点F的上方)．若，

    求点F的坐标．

    查看答案和解析>>

    同步练习册答案