
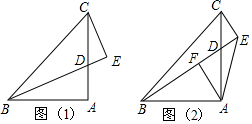
分析 (1)①根据等腰直角三角形的性质得出∠CBA=45°,再利用角平分线的定义解答即可;②延长CE交BA的延长线于点G得出CE=GE,再利用AAS证明△ABD≌△ACG,利用全等三角形的性质解答即可;
(2)过点A作AH⊥AE,交BE于点H,证明△ABH≌△ACE,进而得出CE=BH,利用等腰直角三角形的判定和性质解答即可.
解答 解:(1)①∵在△ABC中,∠BAC=90°,AB=AC,
∴∠CBA=45°,
∵BD平分∠ABC,
∴∠DBA=22.5°,
∵CE⊥BD,
∴∠ECD+∠CDE=90°,∠DBA+∠BDA=90°,
∵∠CDE=∠BDA,
∴∠ECD=∠DBA=22.5°;
②BD=2CE.
证明:延长CE交BA的延长线于点F,如图1,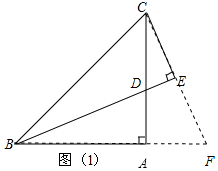
∵BD平分∠ABC,CE⊥BD,
∴CE=FE,
在△ABD与△ACF中,
$\left\{\begin{array}{l}{∠DBA=∠ACF}\\{∠BAC=∠CAF}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACF(AAS),
∴BD=CF=2CE;
(2)结论:BE-CE=2AF.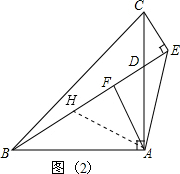
证明:过点A作AH⊥AE,交BE于点H,如图2,
∵AH⊥AE,
∴∠BAH+∠HAC=∠HAC+∠CAE,
∴∠BAH=∠CAE,
在△ABH与△ACE中,
$\left\{\begin{array}{l}{∠HBA=∠ECA}\\{AB=AC}\\{∠BAH=∠ACE}\end{array}\right.$,
∴△ABH≌△ACE(ASA),
∴CE=BH,AH=AE,
∴△AEH是等腰直角三角形,
∴AF=EF=HF,
∴BE-CE=2AF.
点评 本题属于三角形综合题,主要考查的是等腰直角三角形的性质以及全等三角形的判定和性质的综合应用,作辅助线构造出与所求和已知相关的全等三角形,是解答本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 购买一张彩票,中奖 | |
| B. | 打开电视,正在播放广告 | |
| C. | 抛掷一枚硬币,正面向上 | |
| D. | 一个袋中只装有2个黑球,从中摸出一个球是黑球 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com