
【题目】如图,平面直角坐标系中有![]() 三点。
三点。
(1)连接![]() ,若
,若![]()
①线段的长为 (直接写出结果)
②如图1,点![]() 为
为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() 作
作![]() ,且
,且![]() ,当点
,当点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 点不变,
点不变,![]() 点随之运动,连接
点随之运动,连接![]() ,求线段
,求线段![]() 的中点
的中点![]() 的运动路径长;
的运动路径长;
(2)如图2,作![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 延长线于
延长线于![]() 于
于![]() .若
.若![]() ,且
,且![]() ,在平面内是否存在点
,在平面内是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形,若存在,请求出点
为顶点的四边形是平行四边形,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)①![]() ②
②![]() (2)
(2)![]()
【解析】
(1)①由两点的距离公式可得出答案;
②分别作出点D运动到点A,B时的等腰直角三角形DCE,画出运动路径如图,求出E1,E2的坐标,即可求出E1E2的长,则答案可求出;
(2)连接BH,证明∠HBA=45°,过点H作HN⊥AB,求出H点坐标,再根据平行四边形的性质可求出M点坐标.
(1)①∵A(3,0),C(4,1),
∴AC=![]() .
.
故答案为:![]() .
.
②分别作出点D运动到点A,B时的等腰直角三角形DCE,画出运动路径如图,
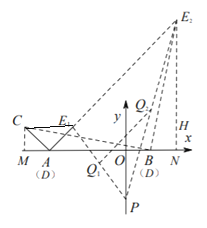
∵C(4,1),△CAE1为等腰直角三角形,A,D重合,A(-3,0)
∴CD=AC=![]() =AE1
=AE1
∴CE1=![]()
∵CE1∥x轴
∴E1(2,1),
分别过点C,E2作x轴的垂线,垂足分别为M,N,
∵∠CBM=∠BE2N,∠CMB=∠BNE2,BC=BE2,
∴△CMB≌△BNE2(AAS),
∴E2N=BM=5,CM=BN=1,
∴E2(2,5),
∴E1E2=![]() .
.
∵Q1Q2为△PE1E2的中位线,
∴线段EP的中点Q的运动路径长Q1Q2=![]() E1E2=2
E1E2=2![]() .
.
(2)如图,连接BH,
∵AF⊥AC,GH⊥CF,
又A(3,0),B(1,0),BF=BG,
∴BH=![]() GF=AB=4,
GF=AB=4,
又∵∠C=67.5°,
∴∠AGB+∠CFB=112.5°,
∴∠ABG+∠HBF=360°2(∠AGB+∠CFB)=135°,
即∠HBA=45°,
过点H作HN⊥AB,∴△BHN是等腰直角三角形,
∴HN=BN,
∴HN=BN=![]() BH=2
BH=2![]() ,
,
∴H(12![]() ,2
,2![]() ),
),
∵A(3,0),B(1,0),
如图,四边形ABM1H是平行四边形时,A平移至B的方式是:向右平移4个单位,
∴H点向右平移4个单位得到M1![]() ;
;
四边形ABH M2是平行四边形时,B平移至A的方式是:向左平移4个单位,
∴H点向右平移4个单位得到M2![]() ;
;
四边形AHBM3是平行四边形时,H平移至B的方式是:向右平移2![]() 个单位,向下平移2
个单位,向下平移2![]() 个单位,
个单位,
∴A点向右平移2![]() 个单位,向下平移2
个单位,向下平移2![]() 个单位M3
个单位M3![]() ;
;
∴使以B,A,H,M为顶点的四边形是平行四边形的点M的坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】综合与实践
问题背景:
我们知道,三角形的中位线平行于三角形的第三边,并且等于第三边的一半,如何证明三角形中位线定理呢?
已知:如图1,在![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.

求证:![]()
问题中既要证明两条线段所在的直线平行,又要证明其中一条线段的长等于另一线段长的一半.所以可以用“倍长法”将![]() 延长一倍:延长
延长一倍:延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() 这样只需证明
这样只需证明![]() ,且
,且![]() .由于
.由于![]() 是
是![]() 的中点,容易证明四边形
的中点,容易证明四边形![]() 、四边形
、四边形![]() 是平行四边形,证明...
是平行四边形,证明...
问题解决:
![]() 上述材料中“倍长法”体现的数学思想主要是_____. (填入选项前的字母代号即可)
上述材料中“倍长法”体现的数学思想主要是_____. (填入选项前的字母代号即可)
A.数形结合思想 B.转化思想 C.分类讨论思想 D.方程思想
![]() 证明四边形
证明四边形![]() 是平行四边形的依据是
是平行四边形的依据是

反思交流:
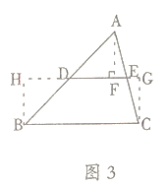
“智慧小组”在证明中位线定理时,在图1的基础上追加了如上辅助线作法:如图3,分别过点![]() 作
作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,..
,..
![]() 请你根据“智慧小组”添加的辅助线,证明三角形的中位线定理.
请你根据“智慧小组”添加的辅助线,证明三角形的中位线定理.
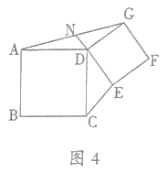
方法迁移:
![]() 如图4、四边形
如图4、四边形![]() 和
和![]() 都是正方形,
都是正方形,![]() 是
是![]() 的中点.求证:
的中点.求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,点D在直线BC上,E在AC上,且AC=CD,DE=AB.
(1)如图②,将△ECD沿CB方向平移,使点E落在AB上,得△E1C1D1,求平移的距离;
(2)如图③,将△ECD绕点C逆时针旋转,使点E落在AB上,得△E2CD2,求旋转角∠DCD2的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
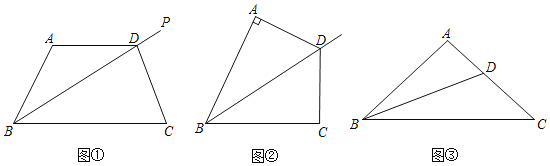
【题目】(问题)如图①,点D是∠ABC的角平分线BP上一点,连接AD,CD,若∠A与∠C互补,则线段AD与CD有什么数量关系?
(探究)
探究一:如图②,若∠A=90°,则∠C=180°﹣∠A=90°,即AD⊥AB,CD⊥BC,又因为BD平分∠ABC,所以AD=CD,理由是: .
探究二:若∠A≠90°,请借助图①,探究AD与CD的数量关系并说明理由.
[理论]点D是∠ABC的角平分线BP上一点,连接AD,CD,若∠A与∠C互补,则线段AD与CD的数量关系是 .
[拓展]已知:如图③,在△ABC中,AB=AC,∠A=100°,BD平分∠ABC.
求证:BC=AD+BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.
与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,-3),点D与点C关于抛物线的对称轴对称.

(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线对称轴上的一动点,当△PAC的周长最小时,求出点P的坐标;
(3)若点Q在x轴正半轴上,且∠ADQ=∠DAC,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD内接于⊙O,如图所示,在劣弧![]() 上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:
上取一点E,连接DE、BE,过点D作DF∥BE交⊙O于点F,连接BF、AF,且AF与DE相交于点G,求证:

(1)四边形EBFD是矩形;
(2)DG=BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,菱形OABC的OC边落在x轴上,∠AOC=60°,OA=60![]() .若菱形OABC内部(边界及顶点除外)的一格点P(x,y)满足:x2﹣y2=90x﹣90y,就称格点P为“好点”,则菱形OABC内部“好点”的个数为( )
.若菱形OABC内部(边界及顶点除外)的一格点P(x,y)满足:x2﹣y2=90x﹣90y,就称格点P为“好点”,则菱形OABC内部“好点”的个数为( )
(注:所谓“格点”,是指在平面直角坐标系中横、纵坐标均为整数的点.)

A. 145 B. 146 C. 147 D. 148
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com