
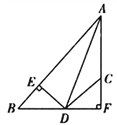
【题目】如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且BD=CD.
(1)图中与△BDE全等的三角形是 ,请加以证明;
(2)若AE=6 cm,AC=4 cm,求BE的长.
【答案】(1)△CDF,证明见解析;(2)2cm
【解析】试题分析:(1)根据角平分线的性质得出DE=DF,再利用HL证明Rt△BED与Rt△DFC全等;
(2)根据全等三角形的性质得出BE=CF,进而解答即可.
试题解析:解:(1)与△BDE全等的三角形是△CDF,证明如下:
∵ AD平分∠BAC,DE⊥AC,∴ DE=FD,∠BED=∠CFD=90°.又BD=CD,∴ Rt△BDE≌Rt△CDF(HL)
(2)∵ AD=AD,DE=DF,∴ Rt△ADE≌Rt△ADF(HL),∴ AE=AF.又AE=6 cm,∴ AF=6 cm.∵ AC=4 cm,∴ CF=AF-AC=2(cm).
由(1)可知BDE≌Rt△CDF,∴BE=CF=2 cm


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D是BC延长线上的一点,线段BD的垂直平分线EG交AB于点E,交BD于点G. 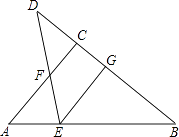
(1)当∠B=30°时,AE和EF有什么关系?请说明理由;
(2)当点D在BC延长线上(CD<BC)运动时,点E是否在线段AF的垂直平分线上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)2×(﹣4)2
(2)(﹣6)×(﹣ ![]() +
+ ![]() )
)
(3)﹣56÷(﹣8)×( ![]() )
)
(4)4.98×(﹣5)
(5)25× ![]() ﹣(﹣25)×
﹣(﹣25)× ![]() +25×(﹣
+25×(﹣ ![]() )
)
(6)(﹣1)4﹣ ![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
(7)(﹣1 ![]() )×
)× ![]() ×8﹣9÷(﹣
×8﹣9÷(﹣ ![]() )2
)2
(8)﹣103+[(﹣4)2﹣(1﹣32)×2].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com