
【题目】在正方形ABCD中,E为CD上一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BCE≌△DCF;
(2)若∠FDC=30°,求∠BEF的度数.

【答案】见解析
【解析】试题分析:
(1) 结合条件观察图形可知,在待求证的这组全等三角形中,有一组对应角∠BCE与∠DCF互补,根据四边形ABCD是正方形的条件易知∠BCE=∠DCF. 以这组对应角为着眼点进一步观察图形易知,作为正方形ABCD边的BC与DC相等,条件中又已知CE=CF,故可以利用SAS证明这组三角形全等.
(2) 求∠BEF的度数就是求∠BEC+∠CEF的度数. 在Rt△DCF中易知∠DFC的度数. 利用第(1)小题的结论可知∠BEC=∠DFC,从而得到∠BEC的度数. 利用条件可以得出△ECF为等腰直角三角形的结论,从而得到∠CEF的度数. 综合上面的结果即得∠BEF的度数.
试题解析:
(1) 证明:∵四边形ABCD是正方形,
∴BC=DC,∠BCD=90°,
∴∠DCF=∠BCD=90°,即∠BCE=∠DCF=90°,
∵在△BCE与△DCF中:
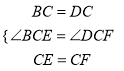 ,
,
∴△BCE≌△DCF (SAS).
(2) ∠BEF的度数为105°. 求解过程如下.
∵∠FDC=30°,∠DCF=90°,
∴在Rt△DCF中,∠DFC=90°-∠FDC=90°-30°=60°,
∵△BCE≌△DCF,
∴∠BEC=∠DFC=60°,
∵CE=CF,∠DCF=90°,
∴△ECF为等腰直角三角形,
∴∠CEF=∠CFE=45°,
∵∠BEC=60°,∠CEF=45°,
∴∠BEF=∠BEC+∠CEF=60°+45°=105°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=![]() (k>0)表示(如图所示).
(k>0)表示(如图所示).

(1)求k的值.(2)假设某驾驶员晚上在家喝完半斤低度白酒,求有多长时间其酒精含量不低于72毫克/百毫升?(用分钟表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,② AQ=BQ,③BP=2PQ, ④AE+BD=AB,其正确的个数有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据崇左市气象预报:我市6月份某天中午各县(区)市的气温如下:
地名 | 江州区 | 扶绥县 | 天等县 | 大新县 | 龙州县 | 宁明县 | 凭祥市 |
气温 | 37(℃) | 33(℃) | 30(℃) | 31(℃) | 33(℃) | 36(℃) | 34(℃) |
则我市各县(区)市这组气温数据的极差是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
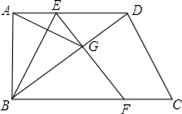
【题目】如图,在梯形ABCD中,∠ABC=∠BAC=90°,在AD上取一点E,将△ABE沿直线BE折叠,使点A落在BD上的G处,EG的延长线交直线BC于点F.
(1)试探究AE、ED、DG之间有何数量关系?说明理由;
(2)判断△ABG与△BFE是否相似,并对结论给予证明;
(3)设AD=a,AB=b,BC=c.
①当四边形EFCD为平行四边形时,求a、b、c应满足的关系;
②在①的条件下,当b=2时,a的值是唯一的,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】挖一条长2020m的水渠,由甲、乙两个施工队从两头相向施工,甲队每天挖130m,乙队每天挖90m,甲队先挖两天,剩下的由两队共同完成,完成这项工程共需多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com