
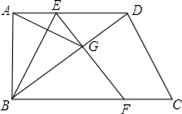
����Ŀ����ͼ��������ABCD�У���ABC=��BAC=90�㣬��AD��ȡһ��E������ABE��ֱ��BE�۵���ʹ��A����BD�ϵ�G����EG���ӳ��߽�ֱ��BC�ڵ�F��
��1����̽��AE��ED��DG֮���к�������ϵ��˵�����ɣ�
��2���жϡ�ABG���BFE�Ƿ����ƣ����Խ��۸���֤����
��3����AD=a��AB=b��BC=c��
�ٵ��ı���EFCDΪƽ���ı���ʱ����a��b��cӦ����Ĺ�ϵ��
���ڢٵ������£���b=2ʱ��a��ֵ��Ψһ�ģ����C�Ķ�����
���𰸡���1��AE2+DG2=ED2�����ɼ���������2����ABG�ס�BFE�����ɼ���������3����a2+b2=ac���ڡ�C=45�㣮
�������������������1�����۵��õ���EGB=��EAB=90�㣬�����ù��ɶ������ɣ�
��2�����жϡ�EAB�ա�EGB��Ȼ���ABG=��EFB�͡�BAG=��FBE�����õȵ����ۣ�
��3���ɣ�2���еĽ��ۡ�ABG�ס�BFE�ó����ۣ����ж�����ABD�ס�HCD�ó�����ʽ�����ҵ����ۣ����ɸ���ϵ���Ĺ�ϵ���жϼ��㼴�ɣ�
�����������1��AE2+DG2=ED2��
���ɣ����۵����ʵã���EAB�ա�EGB��AE=GE����EGB=��EAB=90�㣬
����Rt��EGD�У��ɹ��ɶ����ã�EG2+DG2=ED2��
��AE2+DG2=ED2��
��2����ABG�ס�BFE��
���ɣ��ߡ�ABC=��BAC=90�㣬��AD��BC�����AEB=��EBF��
�ߡ�EAB�ա�EGB����AEB=��BEG�����EBF=��BEF����FE=FB������FEBΪ���������Σ�
�ߡ�ABG+��GBF=90�㣬��GBF+��EFB=90�㣬���ABG=��EFB��
�ڵ�����ABG�͡�FEB�У���BAG=��180��-��ABG����2����FBE=��180��-��EFB����2��
���BAG=��FBE��
���ABG�ס�BFE��
��3���١ߡ�ABG�ס�BFE�����EFB=��GBA�����C=��ABG��
�ߡ�DAB=��DHC=90�㣬���ABD�ס�HCD����![]() ��
��
��![]() ����a2+b2=ac��
����a2+b2=ac��
�ڵ�b=2ʱ�������a��һԪ���η���a2��ac+22=0������Ϊa1��a2��
�ã�a1a2=c��0��a1+a2=4��0����a1��0��a2��0��
������a1=a2�����=0����c2��16=0��
��c��0����c=4����a=2����HΪBC�е㣬��ABHDΪ�����Σ���DH=HC��
���C=45�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=BC����E�ڱ�AB�ϣ�EF��AC��F��

��1���߹���ͼ������A��AD��BC�ڵ�D��������ͼ�ۼ�����д����������2����֤����CAD=��AEF����3������ABC=45����AD��EF���ڵ�G����֤��EG=2AF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
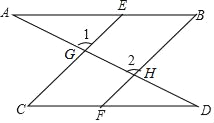
����Ŀ����ͼ��һ��ֱ�߷ֱ���ֱ��BE��ֱ��CE��ֱ��CF��ֱ��BF�ཻ�ڵ�A��G��D��H�ҡ�1=��2����B=��C
��1���ҳ�ͼ���ƽ�е��ߣ�˵˵����֮��Ϊʲô��ƽ�еģ�
��2��֤������A=��D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������ÿ��С�����α߳�����1��
(1)������ABC����ֱ��1�ԳƵ�ͼ����A1BlCl;
(2)��ֱ��l����һ��P��ʹPB=PC;��Ҫ����ֱ��1�ϱ����P��λ�ã�
(3)����PA��PC�������ı���PABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�EΪCD��һ�㣬FΪBC�ӳ�����һ�㣬��CE��CF.
��1����֤����BCE�ա�DCF��
��2������FDC��30�������BEF�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ����2x��2����x��y������3��3����6����x+3x����x��1��2x��3�У�һԪһ�η����У�������
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�DE��AC�ڵ�E����EDC����EDA=1��3����AC=12����DE�ij�����______������ø��ű�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������¾Ӻ�С���Լ������ò���ֽ����һ����ͼ��ʾ�������εĹ�ʽС��ƷABCD������BD��AN��CM��������ABCD�ֳ������֣�����M��AB���е㣬N��BC���е㣬AN��CM����O�㣮��֪������ABCD�����Ϊ576cm2���ָ�������CON�����Ϊ��������

A. 96cm2 B. 48cm2 C. 24cm2 D. ���϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P��������y=2��x��2��2�Գ����ϵ�һ�����㣬ֱ��x=tƽ��y�ᣬ�ֱ���y=x�������߽��ڵ�A��B������ABP���Ե�A���BΪֱ�Ƕ���ĵ���ֱ�������Σ�������������t��ֵ����t= ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com