
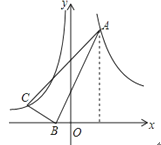
【题目】如图,在Rt△ABC中,∠ABC=90°,点B在x轴上,且B(-1,0),A点的横坐标是2,AB=3BC,双曲线![]() 经过A点,双曲线y=-
经过A点,双曲线y=-![]() 经过C点,则Rt△ABC的面积为_________。
经过C点,则Rt△ABC的面积为_________。
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】线段EF是由线段PQ平移得到的,点P(﹣1,4)的对应点为E(4,7),则点Q(﹣3,1)的对应点F的坐标为()
A.(﹣8,﹣2)
B.(﹣2,﹣2)
C.(2,4)
D.(﹣6,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,∠A=∠D,试说明 AC∥DE 成立的理由.
(下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.)
解:∵AB∥CD (已知)
∴∠A=(两直线平行,内错角相等)
又∵∠A=∠D()
∴∠=∠(等量代换)
∴AC∥DE ()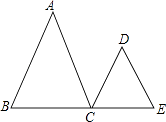
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,且OA,OB的长分别是x2﹣14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒.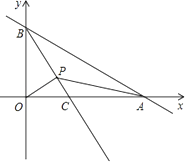
(1)求OA,OB的长;
(2)设△APB和△OPB的面积分别为s1 , s2 , 求s1:s2;
(3)在点P的运动过程中,△OPB可能是等腰三角形吗?若可能,直接写出时间t;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax 2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,顶点为D,点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,则点P的坐标为_______________。
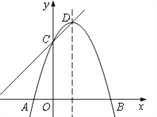
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形的周长为36m,矩形绕着它的一条边旋转形成一个圆柱,设矩形的一条边长为xm,圆柱的侧面积为ym2 , 则y与x的函数关系式为( )
A.y=﹣2πx2+18πx
B.y=2πx2﹣18πx
C.y=﹣2πx2+36πx
D.y=2πx2﹣36πx
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com