
| A. | 2 | B. | 1 | C. | 2017 | D. | 2016 |
分析 观察运算结果找出规律“f(n)=n-1;g($\frac{1}{n}$)=n(n为正整数)”,依此规律即可得出g($\frac{1}{2017}}$)=2017、f(2017)=2017-1,将其代入g($\frac{1}{2017}}$)-f(2017)即可得出结论.
解答 解:观察,发现规律:f(1)=0,f(2)=1,f(3)=2,f(4)=3,…,f(10)=9,…,
∴f(n)=n-1(n为正整数);
g($\frac{1}{2}$)=2,g($\frac{1}{3}}$)=3,g($\frac{1}{4}$)=4,g($\frac{1}{5}}$)=5,…,g($\frac{1}{11}$)=11,…,
∴g($\frac{1}{n}$)=n(n为正整数).
∴g($\frac{1}{2017}}$)-f(2017)=2017-(2017-1)=1.
故选B.
点评 本题考查了规律型中数字的变化类,根据运算结果的变化找出变化规律“f(n)=n-1;g($\frac{1}{n}$)=n(n为正整数)”是解题的关键.


科目:初中数学 来源: 题型:解答题
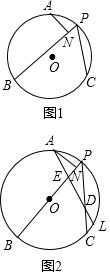 在⊙O中,PB、PC为⊙O的弦,点A在⊙O上,且$\widehat{AB}$=$\widehat{AC}$,过点A作AN⊥PB于点N,
在⊙O中,PB、PC为⊙O的弦,点A在⊙O上,且$\widehat{AB}$=$\widehat{AC}$,过点A作AN⊥PB于点N,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
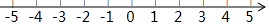
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
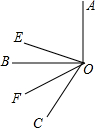 已知:如图∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
已知:如图∠BOC=60°,OE平分∠AOC,OF平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,下列式子正确的是( )| A. | sinA=$\frac{BD}{BC}$ | B. | cosA=$\frac{AC}{AD}$ | C. | tanA=$\frac{CD}{AB}$ | D. | cosB=$\frac{AC}{AB}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购票人数 | 1~50 | 51~100 | 100以上 |
| 每人门票价 | 12 | 10 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com