
【题目】 A、B两地相距45千米,甲汽车以每小时50千米的速度从A地出发,乙汽车以每小时40千米的速度从B地出发
(1)若两车同时出发,相向而行,问经过几小时,两车相距30千米?
(2)若两车同时出发,同向而行,问经过几小时,两车相距30千米?
(3)若乙车先出发半小时,同向而行,则经过几小时,两车相距30千米?
【答案】(1)![]() 小时和
小时和![]() 小时;(2)1.5小时和7.5小时;(3)3.5小时和9.5小时.
小时;(2)1.5小时和7.5小时;(3)3.5小时和9.5小时.
【解析】
(1)首先可设经过x小时,两车相距30千米,本小问要分两种情况进行讨论:①两车相遇前相距30千米;②两车相遇后相距30千米,根据这两种情况列出方程即可;
(2)首先可设经过y小时,两车相距30千米,因为甲车的速度比乙车快,因此本小问要分两种情况进行讨论:①甲车追上乙车前相距30千米;②甲车追上乙车后相距30千米,根据这两种情况列出方程即可;
(3)首先可设经过z小时,两车相距30千米,因为甲车的速度比乙车快,因此本小问要分两种情况进行讨论:①甲车追上乙车前相距30千米;②甲车追上乙车后相距30千米,根据这两种情况列出方程即可.
解:(1)①设经过x小时,两车相遇前相距30千米,依题意,得:
![]() ,
,
解得:![]() .
.
②设经过x小时,两车相遇后相距30千米,依题意,得:
![]() ,
,
解得:![]() .
.
答:经过![]() 小时和经过
小时和经过![]() 小时,两车相距30千米.
小时,两车相距30千米.
(2)①设经过y小时,甲车追上乙车前相距30千米,依题意,得:
![]() ,
,
解得:![]() .
.
②设经过y小时,甲车追上乙车后相距30千米,依题意,得:
![]() ,
,
解得:![]() .
.
答:经过1.5小时和经过7.5小时,两车相距30千米.
(3)①设经过z小时,甲车追上乙车前相距30千米,依题意,得:
![]() ,
,
解得:![]() .
.
②设经过z小时,
![]() ,
,
解得:![]() .
.
答:经过3.5小时和经过9.5小时,两车相距30千米.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
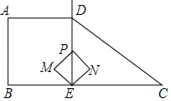
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,射线ED⊥BC于点E,AD=AB=BE=![]() BC=4,动点P从点E出发,沿射线ED以每秒2个单位长度的速度运动,以PE为对角线做正方形PMEN,设运动时间为t秒,正方形PMEN与四边形ABCD重叠部分面积为S.
BC=4,动点P从点E出发,沿射线ED以每秒2个单位长度的速度运动,以PE为对角线做正方形PMEN,设运动时间为t秒,正方形PMEN与四边形ABCD重叠部分面积为S.
(1)当点N落在边DC上时,求t的值.
(2)求S与t的函数关系式.
(3)当正方形PMEN被直线BD分成2:1两部分时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王和小李都想去体育馆,观看在我县举行的“市长杯”青少年校园 足球联赛,但两人只有一张门票,两人想通过摸球的方式来决定谁去观看,规则如下: 在两个盒子内分别装入标有数字 1,2,3,4 的四个和标有数字 1,2,3 的三个完全相 同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于 6,那 么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平.”你认同他的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
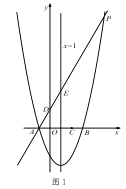
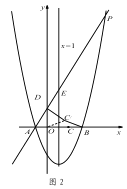
【题目】如图1,对称轴为直线x=1的抛物线y=![]() x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
(1)求点 B 的坐标和抛物线的表达式;
(2)当 AE:EP=1:4 时,求点 E 的坐标;
(3)如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+ ![]() C′D 的最小值.
C′D 的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
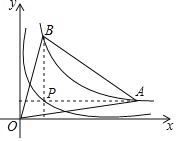
【题目】如图,点P为函数y=![]() (x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y
(x>0)图象上一点过点P作x轴、y轴的平行线,分别与函数y![]() (x>0)的图象交于点A,B,则△AOB的面积为_____.
(x>0)的图象交于点A,B,则△AOB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.
(1)求每行驶1千米纯用电的费用;
(2)若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】首条贯通丝绸之路经济带的高铁线﹣宝兰客专进入全线拉通试验阶段,宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行一下探究:
【信息读取】
(1)西宁到西安两地相距 千米,两车出发后 小时相遇;
(2)普通列车到达终点共需 小时,普通列车的速度是 千米/小时.
【解决问题】
(3)求动车的速度;
(4)普通列车行驶t小时后,动车到达终点西宁,求此时普通列车还需行驶多少千米到达西安?

查看答案和解析>>
科目:初中数学 来源: 题型:
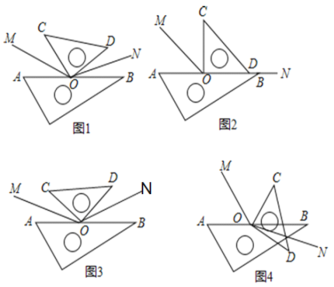
【题目】综合与探究问题背景数学活动课上,老师将一副三角尺按图(1)所示位置摆放,分别作出∠AOC,∠BOD的平分线OM、ON,然后提出如下问题:求出∠MON的度数.
特例探究“兴趣小组”的同学决定从特例入手探究老师提出的问题,他们将三角尺分别按图2、图3所示的方式摆放,OM和ON仍然是∠AOC和∠BOD的角平分线.其中,按图2方式摆放时,可以看成是ON、OD、OB在同一直线上.按图3方式摆放时,∠AOC和∠BOD相等.
(1)请你帮助“兴趣小组”进行计算:图2中∠MON的度数为 °.图3中∠MON的度数为 °.
发现感悟
解决完图2,图3所示问题后,“兴趣小组”又对图1所示问题进行了讨论:
小明:由于图1中∠AOC和∠BOD的和为90°,所以我们容易得到∠MOC和∠NOD的和,这样就能求出∠MON的度数.
小华:设∠BOD为x°,我们就能用含x的式子分别表示出∠NOD和∠MOC度数,这样也能求出∠MON的度数.
(2)请你根据他们的谈话内容,求出图1中∠MON的度数.
类比拓展
受到“兴趣小组”的启发,“智慧小组”将三角尺按图4所示方式摆放,分别作出∠AOC、∠BOD的平分线OM、ON,他们认为也能求出∠MON的度数.
(3)你同意“智慧小组”的看法吗?若同意,求出∠MON的度数;若不同意,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com