
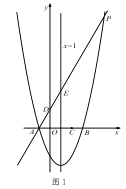
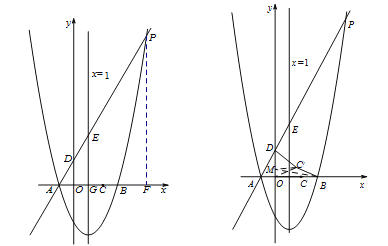
【题目】如图1,对称轴为直线x=1的抛物线y=![]() x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
(1)求点 B 的坐标和抛物线的表达式;
(2)当 AE:EP=1:4 时,求点 E 的坐标;
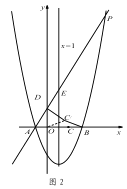
(3)如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+ ![]() C′D 的最小值.
C′D 的最小值.
【答案】(1)B(3,0);抛物线的表达式为:y=![]() x2-x-
x2-x-![]() ;(2)E(1,6);(3)C′B+
;(2)E(1,6);(3)C′B+![]() C′D的最小值为
C′D的最小值为![]() .
.
【解析】试题分析:(1)由抛物线的对称轴和过点A ,即可得到抛物线的解析式,令y=0,解方程可得B的坐标;
(2)过点P作PF⊥x轴,垂足为F.由平行线分线段弄成比例定理可得![]() =
=![]() =
=![]() =
=![]() ,从而求出E的坐标;
,从而求出E的坐标;
(3)由E(1,6)、A(-1,0)可得AP的函数表达式为y=3x+3,得到D(0,3).
如图,取点M(0, ![]() ),连接MC′、BM.则可求出OM,BM的长,得到△MOC′∽△C′OD.进而得到MC′=
),连接MC′、BM.则可求出OM,BM的长,得到△MOC′∽△C′OD.进而得到MC′=![]() C′D,由C′B+
C′D,由C′B+![]() C′D=C′B+MC′≥BF可得到结论.
C′D=C′B+MC′≥BF可得到结论.
试题解析:解:(1)∵抛物线y=![]() x2+bx+c的对称轴为直线x=1,∴-
x2+bx+c的对称轴为直线x=1,∴-![]() =1,∴b=-1.
=1,∴b=-1.
∵抛物线过点A(-1,0),∴![]() -b+c=0,解得:c=-
-b+c=0,解得:c=-![]() ,
,
即:抛物线的表达式为:y=![]() x2-x-
x2-x-![]() .
.
令y=0,则![]() x2/span>-x-
x2/span>-x-![]() =0,解得:x1=-1,x2=3,即B(3,0);
=0,解得:x1=-1,x2=3,即B(3,0);
(2)过点P作PF⊥x轴,垂足为F.
∵EG∥PF,AE:EP=1:4,∴![]() =
=![]() =
=![]() =
=![]() .
.
又∵AG=2,∴AF=10,∴F(9,0).
当x=9时,y=30,即P(9,30),PF=30,∴EG=6,∴E(1,6).
(3)由E(1,6)、A(-1,0)可得AP的函数表达式为y=3x+3,则D(0,3).
∵原点O与点C关于该对称轴成轴对称,∴EG=6,∴C(2,0),∴OC′=OC=2.
如图,取点M(0, ![]() ),连接MC′、BM.则OM=
),连接MC′、BM.则OM=![]() ,BM=
,BM=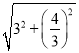 =
=![]() .
.
∵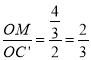 ,
, ![]() ,且∠DOC′=∠C′OD,∴△MOC′∽△C′OD.∴
,且∠DOC′=∠C′OD,∴△MOC′∽△C′OD.∴![]() ,∴MC′=
,∴MC′=![]() C′D,∴C′B+
C′D,∴C′B+![]() C′D=C′B+MC′≥BM=
C′D=C′B+MC′≥BM=![]() ,∴C′B+
,∴C′B+![]() C′D的最小值为
C′D的最小值为![]() .
.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
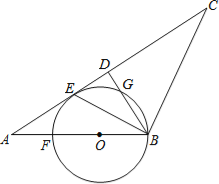
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
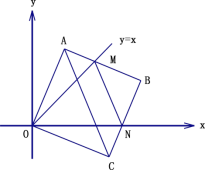
【题目】在平面直角坐标中,边长为 2 的正方形 OABC 的两顶点 A、C 分别在 y 轴、x 轴的正半轴上,点 O 在原点.现将正方形 OABC 绕 O 点顺时针旋转,当 A 点第一次落在直线 y=x 上时停止旋转,旋转过程中,AB 边交直线 y=x于点 M,BC 边交 x 轴于点 N(如图).
(1)求边 OA 在旋转过程中所扫过的面积;
(2)旋转过程中,当 MN 和 AC 平行时,求正方形 OABC 旋转的度数;
(3)试证明在旋转过程中, △MNO 的边 MN 上的高为定值;
(4)设△MBN 的周长为 p,在旋转过程中,p 值是否发生变化?若发生变化,说明理由;若不发生变化,请给予证明,并求出 p 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为1厘米的6个相同正方体摆成如图的形式.
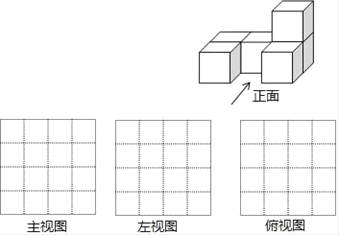
(1)画出该几何体的主视图、左视图、俯视图;
(2)直接写出该几何体的表面积为 cm2(包括底面);
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加 小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3 月初某商品价格上涨,每件价格上涨 20%.用 3000 元买到的该商品 件数比涨价前少 20 件.3 月下旬该商品开始降价,经过两次降价后,该商品价格为每 件 19.2 元.
(1)求 3 月初该商品上涨后的价格;
(2)若该商品两次降价率相同,求该商品价格的平均降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(-1)×2=-2 | (-3)×(-4)×(-5)=-60 | |
三个角上三个数的和 | 1+(-1)+2=2 | (-3)+(-4)+(-5)=-12 | |
积与和的商 | (-2)÷2=-1 |
(2)请用你发现的规律求出图④中的数x和图⑤中的数y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 A、B两地相距45千米,甲汽车以每小时50千米的速度从A地出发,乙汽车以每小时40千米的速度从B地出发
(1)若两车同时出发,相向而行,问经过几小时,两车相距30千米?
(2)若两车同时出发,同向而行,问经过几小时,两车相距30千米?
(3)若乙车先出发半小时,同向而行,则经过几小时,两车相距30千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,随着电子商务的快速发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
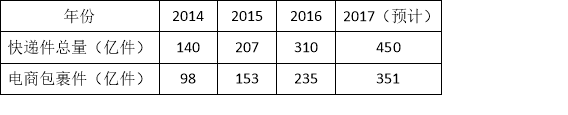
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(精确到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过 ![]() 元的电器,超出的金额按
元的电器,超出的金额按 ![]() 收取;乙商场规定:凡超过
收取;乙商场规定:凡超过 ![]() 元的电器,超出的金额按
元的电器,超出的金额按 ![]() 收取.某顾客购买的电器价格是
收取.某顾客购买的电器价格是 ![]() 元.
元.
(1)当 ![]() 时,该顾客应选择在 商场购买比较合算;
时,该顾客应选择在 商场购买比较合算;
(2)当 ![]() 时,分别用代数式表示在两家商场购买电器所需付的费用;
时,分别用代数式表示在两家商场购买电器所需付的费用;
(3)当 ![]() 时,该顾客应选择哪一家商场购买比较合算?说明理由.
时,该顾客应选择哪一家商场购买比较合算?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com