
【题目】在平面直角坐标中,边长为 2 的正方形 OABC 的两顶点 A、C 分别在 y 轴、x 轴的正半轴上,点 O 在原点.现将正方形 OABC 绕 O 点顺时针旋转,当 A 点第一次落在直线 y=x 上时停止旋转,旋转过程中,AB 边交直线 y=x于点 M,BC 边交 x 轴于点 N(如图).
(1)求边 OA 在旋转过程中所扫过的面积;
(2)旋转过程中,当 MN 和 AC 平行时,求正方形 OABC 旋转的度数;
(3)试证明在旋转过程中, △MNO 的边 MN 上的高为定值;
(4)设△MBN 的周长为 p,在旋转过程中,p 值是否发生变化?若发生变化,说明理由;若不发生变化,请给予证明,并求出 p 的值.
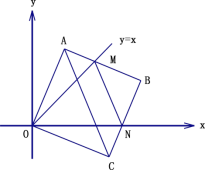
【答案】(1)OA 在旋转过程中所扫过的面积为 0.5π ;(2)旋转过程中,当 MN 和 AC 平行时,正方形 OABC 旋转的度数为 45°-22.5°=22.5 度;(3)MN 边上的高为 2(4)在旋转正方形 OABC 的过程中,p 值无变化.见解析.
【解析】
(1)过点M作MH⊥y轴,垂足为H,如图1,易证∠MOH=45°,然后运用扇形的面积公式就可求出边OA在旋转过程中所扫过的面积.
(2)根据正方形和平行线的性质可以得到AM=CN,从而可以证到△OAM≌△OCN.进而可以得到∠AOM=∠CON,就可算出旋转角∠HOA的度数.
(3)过点O作OF⊥MN,垂足为F,延长BA交y轴于E点,如图2,易证△OAE≌△OCN,从而得到OE=ON,AE=CN,进而可以证到△OME≌△OMN,从而得到∠OME=∠OMN,然后根据角平分线的性质就可得到结论.
(4)由△OME≌△OMN(已证)可得ME=MN,从而可以证到MN=AM+CN,进而可以推出p=AB+BC=4,是定值.
解:(1)过点M作MH⊥y轴,垂足为H,如图1,
∵点M在直线y=x上,
∴OH=MH.
在Rt△OHM中,
∵tan∠MOH=![]() =1,
=1,
∴∠MOH=45°.
∵A点第一次落在直线y=x上时停止旋转,
∴OA旋转了45°.
∵正方形OABC的边长为2,
∴OA=2.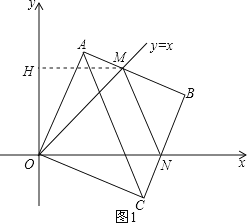
∴OA在旋转过程中所扫过的面积为![]()
![]() =0.5π.∵A 点第一次落在直线 y=x 上时停止旋转, ∴OA 旋转了 45 度.
=0.5π.∵A 点第一次落在直线 y=x 上时停止旋转, ∴OA 旋转了 45 度.
∴OA 在旋转过程中所扫过的面积为 0.5π .
(2)∵MN∥AC, ∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45 度.
∴∠BMN=∠BNM.BM=BN.
又∵BA=BC,AM=CN.
又∵OA=OC,∠OAM=∠OCN,
∴△OAM ≌△OCN. ∴∠AOM=∠CON.
∴∠AOM= 1/2(90°-45°)=22.5 度.
∴旋转过程中,当 MN 和 AC 平行时,正方形 OABC 旋转的度数为 45°-22.5°=22.5 度.
(3)证明:过点O作OF⊥MN,垂足为F,延长BA交y轴于E点,如图2,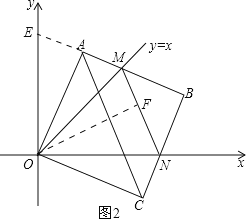
则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM.
∴∠AOE=∠CON.
在△OAE和△OCN中,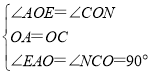 .
.
∴△OAE≌△OCN(ASA).
∴OE=ON,AE=CN.
在△OME和△OMN中
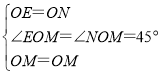
∴△OME≌△OMN(SAS).
∴∠OME=∠OMN.
∵MA⊥OA,MF⊥OF,
∴OF=OA=2.
∴在旋转过程中,△MNO的边MN上的高为定值.MN 边上的高为 2;
(4)在旋转正方形OABC的过程中,p值不变化.
证明:延长 BA 交 y 轴于
∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN.
∴△OAE ≌△OCN.
∴OE=ON,AE=CN.
又 ∵∠MOE=∠MON=45°,OM=OM,
∴△OME ≌△OMN.
∴MN=ME=AM+AE. ∴MN=AM+CN,
∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.
∴在旋转正方形 OABC 的过程中,p 值无变化.
故答案为:(1)OA 在旋转过程中所扫过的面积为 0.5π ;(2)旋转过程中,当 MN 和 AC 平行时,正方形 OABC 旋转的度数为 45°-22.5°=22.5 度;(3)MN 边上的高为 2(4)在旋转正方形 OABC 的过程中,p 值无变化.见解析.


科目:初中数学 来源: 题型:
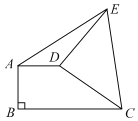
【题目】如图 ,直角梯形 ABCD 中, AD ∥ BC , AB ⊥ BC,AD 2 ,将腰CD 以点 D 为中心逆时针旋转 90°至 DE ,连接 AE、CE ,△ADE 的面积为 3,则 BC 的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
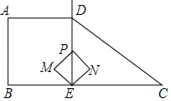
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,射线ED⊥BC于点E,AD=AB=BE=![]() BC=4,动点P从点E出发,沿射线ED以每秒2个单位长度的速度运动,以PE为对角线做正方形PMEN,设运动时间为t秒,正方形PMEN与四边形ABCD重叠部分面积为S.
BC=4,动点P从点E出发,沿射线ED以每秒2个单位长度的速度运动,以PE为对角线做正方形PMEN,设运动时间为t秒,正方形PMEN与四边形ABCD重叠部分面积为S.
(1)当点N落在边DC上时,求t的值.
(2)求S与t的函数关系式.
(3)当正方形PMEN被直线BD分成2:1两部分时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下![]() +
+![]() =
=![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得![]() +
+![]() =
=![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,b)是“相伴数对”,求b的值;
(2)写出一个“相伴数对”(a,b),其中a,b为整数且a≠0;
(3)若(m,n)是“相伴数对”,求代数式m﹣![]() n﹣[4m﹣2(3n﹣1)]的值.
n﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为民中学租用两辆速度相同的小汽车送1名带队老师和6名学生到城区中学参加数学竞赛,每辆限坐4人(不包括司机).其中一辆小汽车在距离考场16.5 km的地方出现故障,此时离截止进考场的时刻还有50分钟,这时唯一可利用的交通工具是另一辆小汽车,且这辆车的平均速度是55 km/h,人步行的速度是5 km/h(上、下车时间忽略不计).
(1)若小汽车送4人到达考场,然后再回到出故障处接其他人,请你通过计算说明他们能否在截止进考场的时刻前到达考场;
(2)假如你是带队的老师,请设计一种你认为较优的运送方案,使他们能在截止进考场的时刻前到达考场,并通过计算说明方案的可行性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王和小李都想去体育馆,观看在我县举行的“市长杯”青少年校园 足球联赛,但两人只有一张门票,两人想通过摸球的方式来决定谁去观看,规则如下: 在两个盒子内分别装入标有数字 1,2,3,4 的四个和标有数字 1,2,3 的三个完全相 同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于 6,那 么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平.”你认同他的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
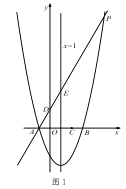
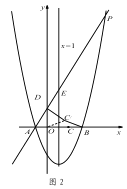
【题目】如图1,对称轴为直线x=1的抛物线y=![]() x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
(1)求点 B 的坐标和抛物线的表达式;
(2)当 AE:EP=1:4 时,求点 E 的坐标;
(3)如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+ ![]() C′D 的最小值.
C′D 的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】首条贯通丝绸之路经济带的高铁线﹣宝兰客专进入全线拉通试验阶段,宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义.试运行期间,一列动车从西安开往西宁,一列普通列车从西宁开往西安,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象进行一下探究:
【信息读取】
(1)西宁到西安两地相距 千米,两车出发后 小时相遇;
(2)普通列车到达终点共需 小时,普通列车的速度是 千米/小时.
【解决问题】
(3)求动车的速度;
(4)普通列车行驶t小时后,动车到达终点西宁,求此时普通列车还需行驶多少千米到达西安?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com