
【题目】如图,已知![]() 的顶点A、C分别在直线
的顶点A、C分别在直线![]() 和
和![]() 上,O是坐标原点,则对角线OB长的最小值为( )
上,O是坐标原点,则对角线OB长的最小值为( )
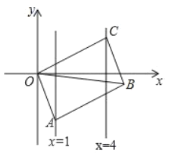
A. 4B. 5C. 6D. 7
【答案】B
【解析】
当B在x轴上时,对角线OB长度最小,由题意得出∠ADO=∠CED=90°,OD=1,OE=4,由平行四边形的性质得出OA∥BC,OA=BC,得出∠AOD=∠CBE,由AAS证明△AOD≌△CBE,得出OD=BE=1,即可得出结果.
当B在x轴上时,对角线OB长度最小,如图所示:
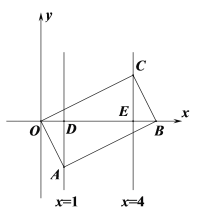
直线x=1与x轴交于点D,直线x=4与x轴交于点E,
根据题意得:∠ADO=∠CEB=90°,OD=1,OE=4,
四边形ABCD是平行四边形,
∴OA∥BC,OA=BC,
∴∠AOD=∠CBE,
在△AOD和△CBE中,
 ,
,
∴△AOD≌△CBE(AAS),
∴OD=BE=1,
∴OB=OE+BE=5,
故答案为:5.


科目:初中数学 来源: 题型:
【题目】已知下列方程,属于一元一次方程的有( )
①x﹣2=![]() ;②0.5x=1;③
;②0.5x=1;③![]() =8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.
=8x﹣1;④x2﹣4x=8;⑤x=0;⑥x+2y=0.
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):![]() .问:
.问:
(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 是
是 ![]() 内一点,
内一点, ![]() 与
与 ![]() 相交于
相交于 ![]() 、
、![]() 两点,且与
两点,且与 ![]() 、
、![]() 分别相切于点
分别相切于点 ![]() 、
、![]() ,
, ![]() .连接
.连接 ![]() 、
、![]() .
.
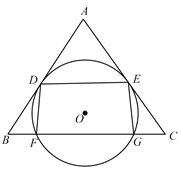
(1)求证: ![]() .
.
(2)已知 ![]() ,
, ![]() .求四边形
.求四边形 ![]() 是矩形时
是矩形时 ![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
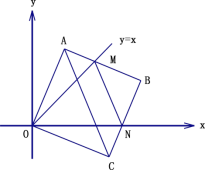
【题目】在平面直角坐标中,边长为 2 的正方形 OABC 的两顶点 A、C 分别在 y 轴、x 轴的正半轴上,点 O 在原点.现将正方形 OABC 绕 O 点顺时针旋转,当 A 点第一次落在直线 y=x 上时停止旋转,旋转过程中,AB 边交直线 y=x于点 M,BC 边交 x 轴于点 N(如图).
(1)求边 OA 在旋转过程中所扫过的面积;
(2)旋转过程中,当 MN 和 AC 平行时,求正方形 OABC 旋转的度数;
(3)试证明在旋转过程中, △MNO 的边 MN 上的高为定值;
(4)设△MBN 的周长为 p,在旋转过程中,p 值是否发生变化?若发生变化,说明理由;若不发生变化,请给予证明,并求出 p 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为1厘米的6个相同正方体摆成如图的形式.
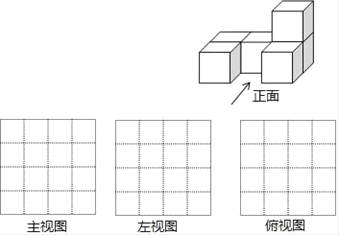
(1)画出该几何体的主视图、左视图、俯视图;
(2)直接写出该几何体的表面积为 cm2(包括底面);
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加 小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(-1)×2=-2 | (-3)×(-4)×(-5)=-60 | |
三个角上三个数的和 | 1+(-1)+2=2 | (-3)+(-4)+(-5)=-12 | |
积与和的商 | (-2)÷2=-1 |
(2)请用你发现的规律求出图④中的数x和图⑤中的数y.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线,且∠AOC=40°,∠BON=25°.
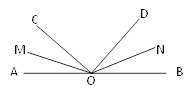
求:(1)∠COD的度数;
(2)∠MON的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com