

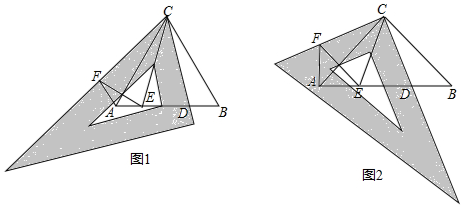
���� ��1�������õȱ������ε�����֤����OBC�ա�ABD��
��֤����OBA=��BAD=60�㣬�ɵ�OB��AD��
��2����֤��DE��BC������ֱ��AE�������ߵĽ�����ǵ�P�����Էֱ���ֱ��AE��������y1�Ľ���ʽ��ɷ����飬��⼴�ɣ���OB��AD�á�OBE��ֱ�������Σ�����P��O�غ�ʱ�������BEPΪֱ����������BEΪֱ�DZߣ�
��3���Ȼ�����ͼ3������ͼ�λ���ֱ����ͼ��M�и�������ʱ�������߽��ֱ�ߣ��Ϸ���y=$\sqrt{3}$x����y=$\sqrt{3}$x����ƽ�Ƽ�������l��ͼ��M��3�������㣬һֱ��ֱ��l��y2����Ϊֹ����Ҫ��������ʱ���з����飬ȷ������0ʱ��m��ֵ���ɣ�
��� 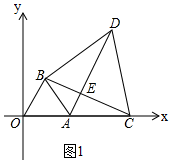 �⣺��1���١�OBC���ABDȫ�ȣ�
�⣺��1���١�OBC���ABDȫ�ȣ�
�����ǣ���ͼ1���ߡ�OAB�͡�BCD�ǵȱ������Σ�
���OBA=��CBD=60�㣬
OB=AB��BC=BD��
���OBA+��ABC=��CBD+��ABC��
����OBC=��ABD��
���OBC�ա�ABD��SAS����
�ڡߡ�OBC�ա�ABD��
���BAD=��BOC=60�㣬
���OBA=��BAD��
��OB��AD��
�����۵�C����ƶ���ADʼ����OBƽ�У�
��2����ͼ2����AC2=AE•AD��
��$\frac{AC}{AD}=\frac{AE}{AC}$��
�ߡ�EAC=��DAC��
���AEC�ס�ACD��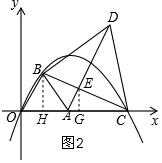
���ECA=��ADC��
�ߡ�BAD=��BAO=60�㣬
���DAC=60�㣬
�ߡ�BED=��AEC��
���ACB=��ADB��
���ADB=��ADC��
��BD=CD��
��DE��BC��
Rt��ABE�У���BAE=60�㣬
���ABE=30�㣬
��AE=$\frac{1}{2}$AB=$\frac{1}{2}$��2=1��
Rt��AEC�У���EAC=60�㣬
���ECA=30�㣬
��AC=2AE=2��
��C��4��0����
�ȱߡ�OAB�У���B��BH��x����H��
��BH=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$��
��B��1��$\sqrt{3}$����
��y1�Ľ���ʽΪ��y=ax��x-4����
��B��1��$\sqrt{3}$������ã�$\sqrt{3}$=a��1-4����
a=-$\frac{\sqrt{3}}{3}$��
����y1�Ľ���ʽΪ��y1=-$\frac{\sqrt{3}}{3}$x��x-4��=-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x��
��E��EG��x����G��
Rt��AGE��AE=1��
��AG=$\frac{1}{2}$AE=$\frac{1}{2}$��
EG=$\sqrt{{1}^{2}-��\frac{1}{2}��^{2}}$=$\frac{\sqrt{3}}{2}$��
��E��$\frac{5}{2}$��$\frac{\sqrt{3}}{2}$����
��ֱ��AE�Ľ���ʽΪ��y=kx+b��
��A��2��0����E��$\frac{5}{2}$��$\frac{\sqrt{3}}{2}$������ã�$\left\{\begin{array}{l}{2k+b=0}\\{\frac{5}{2}k+b=\frac{\sqrt{3}}{2}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=-2\sqrt{3}}\end{array}\right.$��
��ֱ��AE�Ľ���ʽΪ��y=$\sqrt{3}$x-2$\sqrt{3}$��
��$\left\{\begin{array}{l}{y=\sqrt{3}x-2\sqrt{3}}\\{y=-\frac{\sqrt{3}}{3}{x}^{2}+\frac{4\sqrt{3}}{3}}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{{x}_{1}=3}\\{{y}_{1}=\sqrt{3}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=-2}\\{{y}_{2}=-4\sqrt{3}}\end{array}\right.$��
��P��3��$\sqrt{3}$����-2��-4$\sqrt{3}$����
�ɣ�2��֪��OB��AD��
���OBE=��AEC=90�㣬
���OBE��ֱ�������Σ�
��P�ڵ�O��ʱ��Ҳ����������
������������P����������3��$\sqrt{3}$����-2��-4$\sqrt{3}$����0��0����
��3����ͼ3��
y1=-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x=-$\frac{\sqrt{3}}{3}$��x-2��2+$\frac{4\sqrt{3}}{3}$��
���㣨2��$\frac{4\sqrt{3}}{3}$����
��������y2�Ķ���Ϊ��2��-$\frac{4\sqrt{3}}{3}$����
��y2=$\frac{\sqrt{3}}{3}$��x-2��2-$\frac{4\sqrt{3}}{3}$��
��ֱ��y=$\sqrt{3}$x+$\sqrt{3}$m�����ͼ��M��������y1�����������һ�������û�н��㣬
������y2�����������һ�������û�н��㣬
Ҫͼ��M��ֱ��y=$\sqrt{3}$x+$\sqrt{3}$mֻ��3�����㣬��ֱ��y=$\sqrt{3}$x+$\sqrt{3}$m��y1��y2���У�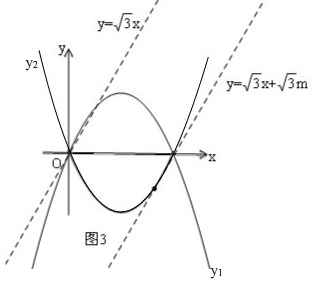
��y2��l����ʱ��ֱ��l��y2ֻ��һ�������㣬����l��ͼ��M��3�������㣬
��$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{3}��x-2��^{2}-\frac{4\sqrt{3}}{3}}\\{y=\sqrt{3}x+\sqrt{3}m}\end{array}\right.$��
$\sqrt{3}x+\sqrt{3}m$=$\frac{\sqrt{3}}{3}��x-2��^{2}$-$\frac{4\sqrt{3}}{3}$��
x2-7x-3m=0��
��=��-7��2-4��1����-3m��=0��
m=-$\frac{49}{12}$��
��y1��l����ʱ��ֱ��l��y1ֻ��һ�������㣬l��ͼ��M��3�������㣬
��$\left\{\begin{array}{l}{y=-\frac{\sqrt{3}}{3}��x-2��^{2}+\frac{4\sqrt{3}}{3}}\\{y=\sqrt{3}x+\sqrt{3}m}\end{array}\right.$��
��x2-x+3m=0��
���=1-12m=0��
��m=$\frac{1}{12}$��
��ֱ�߾�����0��0����4��0��ʱ��Ҳ�������⣬��ʱm=0��-4
�൱l��M�Ĺ�����Ϊ3��ʱ��m��ȡֵ�ǣ�m=-$\frac{49}{12}$��m=$\frac{1}{12}$��0��-4��
���� �����Ƕ��κ����������ε��ۺ��⣬�����˵ȱ������ε����ʡ�������ȫ�Ⱥ����Ƶ����ʺ��ж���ƽ���ߵ��ж����������Ľ������⡢���۱任�����ô���ϵ���������Ľ���ʽ��֪ʶ���Ƚϸ��ӣ��������������ǵ����ʣ��������ν�ϵ�˼���������������⣬������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������һСʱ�����������С���������������գ�ij����ί��֯��Ա���ڶ��ڳ������̵�̬�Ƚ���������������飬��Ҫ������̬�ȣ�A���˿ͳ�����ֹ��B��Ȱ˵�������ң�C�������ϰ������ֹ��D������ν������������������������������ͳ��ͼ���������ͼ�е���Ϣ�ش��������⣺
������һСʱ�����������С���������������գ�ij����ί��֯��Ա���ڶ��ڳ������̵�̬�Ƚ���������������飬��Ҫ������̬�ȣ�A���˿ͳ�����ֹ��B��Ȱ˵�������ң�C�������ϰ������ֹ��D������ν������������������������������ͳ��ͼ���������ͼ�е���Ϣ�ش��������⣺| ̬�� | A���˿ͳ�����ֹ | B��Ȱ˵�������� | C�������ϰ������ֹ | D������ν |
| Ƶ���������� | 90 | 200 | 30 | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
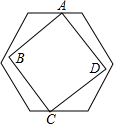 ��ͼ����һ���߳�������������ABCD������������ԵĶ���A��C�ֱ��ڱ߳�Ϊ1����������һ��ƽ�еĶԱ��ϣ�������������B��D�����������ڲ��������߽磩���������α߳�a��ȡֵ��Χ��$\frac{\sqrt{6}}{2}$��a��3-$\sqrt{3}$��
��ͼ����һ���߳�������������ABCD������������ԵĶ���A��C�ֱ��ڱ߳�Ϊ1����������һ��ƽ�еĶԱ��ϣ�������������B��D�����������ڲ��������߽磩���������α߳�a��ȡֵ��Χ��$\frac{\sqrt{6}}{2}$��a��3-$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 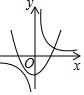 | B�� | 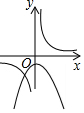 | C�� | 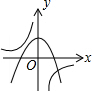 | D�� | 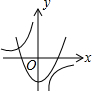 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
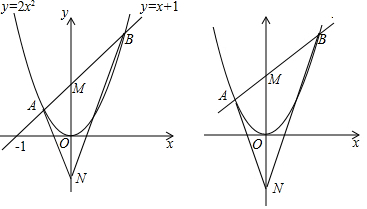
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com