
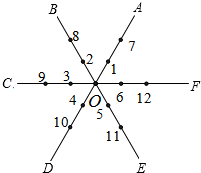
 如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字 1,2,3,4,5,6,7,…
如图,平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字 1,2,3,4,5,6,7,…分析 观察不难发现,每6个数为一个循环组依次循环,数字除以6,根据商和余数的情况确定数所在的射线即可.
(1)17÷6=2…5,得到“17”和“5”在同一条射线上,即射线OE上;
(2)根据射线OA上所有的数除以6的余数为1,射线OB上所有的数除以6的余数为2,射线OC上所有的数除以6的余数为3,射线OD上所有的数除以6的余数为4,射线OE上所有的数除以6的余数为5,射线OF上所有的数除以6的余数为0,即整除,分别得出每条线上的数的排列规律;
(3)根据2014÷6=335…4,得到“2014”和“4”在同一条射线上,即射线OD上.
解答 解:(1)“17”在射线OE上;
(2)射线OA上数字的排列规律:6n-5(n≥1),
射线OB上数字的排列规律:6n-4(n≥1),
射线OC上数字的排列规律:6n-3(n≥1),
射线OD上数字的排列规律:6n-2(n≥1),
射线OE上数字的排列规律:6n-1(n≥1),
射线OF上数字的排列规律:6n(n≥1);
(3)2014÷6=335余4,“2014”与“4”所在的射线相同,是射线OD.
点评 此题考查图形的变化规律,观察图形,得到每6个数为一个循环组依次循环是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com