
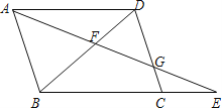
【题目】如图,E为ABCD的边BC延长线上一点,AE与BD交于点F,与DC交于点G.
(1)写出所有与△ABE相似的三角形,并选择其中一对相似三角形加以证明;
(2)若BC=2CE,求![]() 的值.
的值.
【答案】(1)①△ABE∽△GCE,②△ABE∽△GDA(2)![]()
【解析】
(1)根据“平行四边形的对边相互平行”可以推知AB∥DC,所以由平行线的性质得到,∠ABE=∠GCE,∠BAE=∠CGE,则△ABE∽△GCE;根据“平行四边形的对角相等.对边相互平行”可以推知:∠ABE=∠GDA,AD∥BE,根据平行线的性质得到∠E=∠DAG,则易证△ABE∽△GDA;
(2)易证得△ADF∽△EBF,根据相似三角形的对应边成比例可得![]() ,又由BC=2CE,即可求得
,又由BC=2CE,即可求得![]() 的值.
的值.
(1)①△ABE∽△GCE,②△ABE∽△GDA.
①证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∴∠ABE=∠GCE,∠BAE=∠CGE,
∴△ABE∽△GCE.
②证明:∵四边形ABCD是平行四边形,
∴∠ABE=∠GDA,AD∥BE,
∴∠E=∠DAG,
∴△ABE∽△GDA.
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△ADF∽△EBF,
∴![]() =
=![]() ,
,
∵BC=2CE,
∴AD:BE=2:3,
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
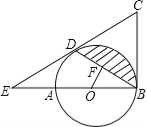
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
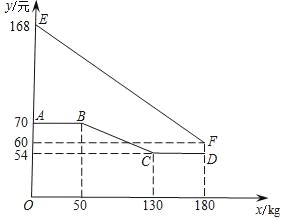
【题目】绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.
(1)求该产品销售价y1(元)与产量x(kg)之间的函数关系式;
(2)直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.

(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )
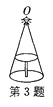
A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A.B在反比例函数y=![]() 的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
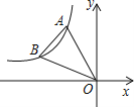
A.5B.-5C.4D.-4
查看答案和解析>>
科目:初中数学 来源: 题型:
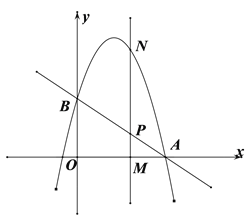
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() ,与y轴交于点B,抛物线
,与y轴交于点B,抛物线![]() 经过点
经过点![]() .
.
![]() 求k的值和抛物线的解析式;
求k的值和抛物线的解析式;
![]() 为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点
为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点![]() .
.
![]() 若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
若以O,B,N,P为顶点的四边形OBNP是平行四边形时,求m的值.
![]() 当
当![]() 时,求m的值.
时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
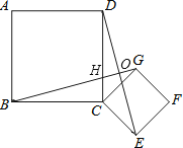
【题目】如图,四边形ABCD和四边形CEFG都是正方形,且BC=CD,CE=CG,∠BCD=∠GCE=90°.
(1)求证:△BCG≌△DCE;
(2)求证:BG⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
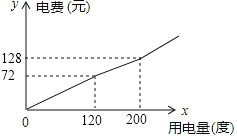
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com