
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
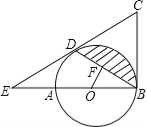
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
【答案】解:(1)证明:连接OD,
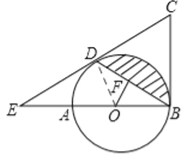
∵BC是⊙O的切线,∴∠ABC=90°。
∵CD=CB,∴∠CBD=∠CDB。
∵OB=OD,∴∠OBD=∠ODB。
∴∠ODC=∠ABC=90°,即OD⊥CD。
∵点D在⊙O上,∴CD为⊙O的切线。
(2)在Rt△OBF中,∵∠ABD=30°,OF=1,∴∠BOF=60°,OB=2,BF=![]() 。
。
∵OF⊥BD,∴BD=2BF=2![]() ,∠BOD=2∠BOF=120°,
,∠BOD=2∠BOF=120°,
∴![]() 。
。
【解析】(1)连接OD,由BC是⊙O的切线,可得∠ABC=90°,由CD=CB,OB=OD,易证得∠ODC=∠ABC=90°,即可证得CD为⊙O的切线。
(2)在Rt△OBF中,∠ABD=30°,OF=1,可求得BD的长,∠BOD的度数,又由![]() ,即可求得答案。
,即可求得答案。


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)|﹣3|+(2018﹣π)0﹣![]() +(
+(![]() )﹣1
)﹣1
(2)化简:(a+1)2﹣a(a﹣2)
(3)解方程:x2+4x﹣5=0;
(4)2x2﹣3x﹣1=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点B、C的坐标分别为(3,4)、(4,2),且AB平行于x轴,将Rt△ABC向左平移,得到Rt△A′B′C′.若点B′、C′同时落在函数y=![]() (x>0)的图象上,则k的值为( )
(x>0)的图象上,则k的值为( )
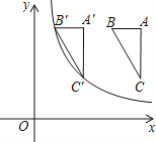
A.2B.4C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
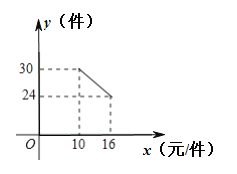
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
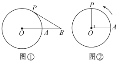
【题目】如图①②,A是半径为12cm的☉O上的定点,动点P从A出发,以2π(cm/s)的速度沿圆周逆时针运动,当点P回到A时立即停止运动.
(1)如图①,点B是OA延长线上一点,AB=OA,当点P运动时间为2s时,试证明直线BP是☉O的切线.
(2)如图②,当∠POA=90°时,求点P的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机动车出发前油箱内有42升油,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示.回答下列问题:
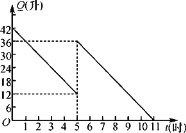
(1)机动车行驶几小时后,在途中加油站加油?
(2)求加油前油箱剩余油量Q与行驶时间t的函数关系,并求自变量t的取值范围;
(3)中途加油多少升?
(4)如果加油站距目的地还有320千米,车速为60千米/时,要到达目的地,油箱中的油是否够用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
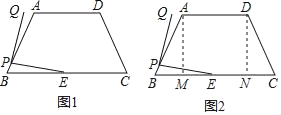
【题目】如图1,在四边形ABCD中,AD∥BC,AB=CD=13,AD=11,BC=21,E是BC的中点,P是AB上的任意一点,连接PE,将PE绕点P逆时针旋转90°得到PQ.
(1)如图2,过A点,D点作BC的垂线,垂足分别为M,N,求sinB的值;
(2)若P是AB的中点,求点E所经过的路径弧EQ的长(结果保留π);
(3)若点Q落在AB或AD边所在直线上,请直接写出BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com