
【题目】如图①②,A是半径为12cm的☉O上的定点,动点P从A出发,以2π(cm/s)的速度沿圆周逆时针运动,当点P回到A时立即停止运动.
(1)如图①,点B是OA延长线上一点,AB=OA,当点P运动时间为2s时,试证明直线BP是☉O的切线.
(2)如图②,当∠POA=90°时,求点P的运动时间.
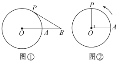
【答案】(1)见解析;(2)当∠POA=90°时,点P运动的时间为3 s或9 s
【解析】
(1)直线BP与⊙O的位置关系是相切,根据已知可证得OP⊥BP,即直线BP与⊙O相切;
(2)当∠POA=90°时,点P运动的路程为⊙O周长的 14或 34,所以分两种情况进行分析.
(2)如图,当点P运动的时间为2s时,直线BP与⊙O相切.理由如下:
当点P运动的时间为2s时,点P运动的路程为4πcm,连接OP,PA,
∵⊙O的周长为24πcm,
∴弧AP的长为⊙O周长的![]() ,
,
∴∠POA=60°;
∵OP=OA,
∴△OAP是等边三角形,
∴OP=OA=AP,∠OAP=60°;
∵AB=OA,
∴AP=AB,
∵∠OAP=∠APB+∠B,
∴∠APB=∠B=30°,
∴∠OPB=∠OPA+∠APB=90°,
∴OP⊥BP,
∴直线BP与⊙O相切;
(2)当∠POA=90°时,点P运动的路程为⊙O周长的![]() 或
或![]() ,
,
设点P运动的时间为ts;
当点P运动的路程为⊙O周长的![]() 时,2πt=
时,2πt=![]() 2π12,
2π12,
解得t=3;
当点P运动的路程为⊙O周长的![]() 时,2πt=
时,2πt=![]() 2π12,
2π12,
解得t=9;
∴当∠POA=90°时,点P运动的时间为3s或9s.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BF平分∠ABC,交CD于点E,交AC于点F.若AB=10,BC=6,则CE的长为( )

A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.

(1)求证:①△BCG≌△DCE;②BH⊥DE.
(2)当点G运动到什么位置时,BH垂直平分DE?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
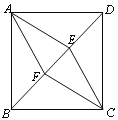
【题目】如图,在正方形ABCD中,点E、F在对角线BD上,且BF=DE.
⑴求证:四边形AECF是菱形.
⑵若AB=2,BF=1,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
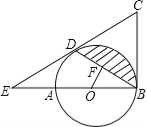
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
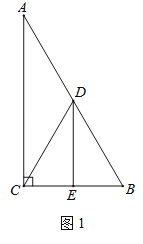
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;

(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
京通公交快速通道开通后,为响应市政府“绿色出行”的号召,家住通州新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米.他用乘公交车的方式平均每小时行驶的路程比他自用驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶多少千米?
.小王用自驾车方式上班平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
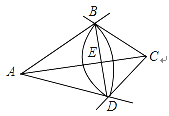
【题目】如图,在![]() 中,按如下步骤作图:
中,按如下步骤作图:
①以点A为圆心,AB长为半径画弧;
②以点C为圆心,CB长为半径画弧,两弧相交于点D;
③连接BD,与AC交于点E,连接AD、CD;
(1)求证:![]() ;
;
(2)当![]() 时,猜想四边形ABCD是什么四边形,并证明你的结论;
时,猜想四边形ABCD是什么四边形,并证明你的结论;
(3)当![]() ,
,![]() ,现将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长是多少?
,现将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于2微克/毫升的持续时间多少小时?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com