练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知正方形ABCD的边长为1，G为CD边上的一个动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H.

    （1）求证：①△BCG≌△DCE；②BH⊥DE.

    （2）当点G运动到什么位置时，BH垂直平分DE？请说明理由.

    【答案】（1）见解析 （2）当时，垂直平分，分析即可求得：时，垂直平分

    【解析】

    （1）由四边形ABCD和四边形CEFG是正方形，根据正方形的性质，即可得BC=DC，CG=CE，∠BCD=∠ECG=90°，则可根据SAS证得①△BCG≌△DCE；然后根据全等三角形的对应角相等，求得∠CDE+∠DHG=90°，则可得②BH⊥DE．

    （2）由当BD=BE时，BH垂直平分DE，分析求即可得：当DG=CG时，BH垂直平分DE。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在社会主义新农村建设中，某乡镇决定对一段公路进行改造，已知这项工程由甲工程队单独做需要40天完成；如果由乙工程先单独做10天，那么剩下的工程还需要两队合做20天才能完成．

    （1）求乙工程队单独完成这项工程所需的天数；

    （2）求两队合作完成这项工程所需的天数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知平面直角坐标系中，△ABC的三个顶点的坐标分别为A（2，2），B（1，﹣1），C（3，0）．

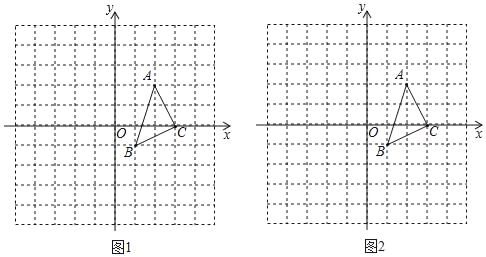
    （1）在图1中，画出以点O为位似中心，放大△ABC到原来的2倍的△A1B1C1；

    （2）若P（a，b）是AB边上一点，平移△ABC之后，点P的对应点P'的坐标是（a+3，b﹣2），在图2中画出平移后的△A2B2C2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，边长为12的等边三角形ABC中，M是高CH所在直线上的一个动点，连结MB，将线段BM绕点B逆时针旋转60°得到BN，连结HN．则在点M运动过程中，线段HN长度的最小值是（ ）

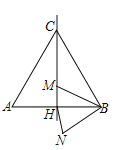
    A.6B.3C.2D.1．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：（1）|﹣3|+（2018﹣π）0﹣+（）﹣1

    （2）化简：（a+1）2﹣a（a﹣2）

    （3）解方程：x2+4x﹣5=0；

    （4）2x2﹣3x﹣1=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

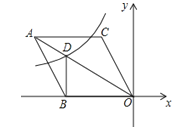
    【题目】如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，∠BOC=60°，顶点C的坐标为（m，），反比例函数的图像与菱形对角线AO交于D点，连接BD，当BD⊥x轴时，k的值是（　　）

    A. B. － C. D. －

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，Rt△ABC的顶点B、C的坐标分别为(3，4)、(4，2)，且AB平行于x轴，将Rt△ABC向左平移，得到Rt△A′B′C′．若点B′、C′同时落在函数y=（x＞0）的图象上，则k的值为（ ）

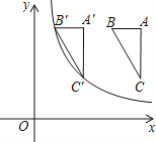
    A.2B.4C.6D.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

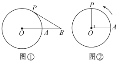
    【题目】如图①②,A是半径为12cm的☉O上的定点,动点P从A出发,以2π(cm/s)的速度沿圆周逆时针运动,当点P回到A时立即停止运动.

    (1)如图①,点B是OA延长线上一点,AB=OA,当点P运动时间为2s时,试证明直线BP是☉O的切线.

    (2)如图②,当∠POA=90°时,求点P的运动时间.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了调查今年有多少名学生参加中考，小明从全市所有家庭中随机抽查了200个家庭，发现其中有10个家庭有子女参加中考。

    （1）本次抽查的200个家庭中，有子女参加中考的家庭的频率是多少？

    （2）如果你随机调查一个家庭，估计该家庭有子女参加中考的概率是多少？

    （3）已知全市约有1.3×106个家庭，假设有子女参加中考的每个家庭中只有一名考生，请你估计今年全市有多少名考生参加中考？

    查看答案和解析>>

    同步练习册答案