
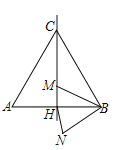
【题目】如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是( )
A.6B.3C.2D.1.5
【答案】B
【解析】
取CB的中点G,连接MG,根据等边三角形的性质可得BH=BG,再求出∠HBN=∠MBG,根据旋转的性质可得MB=NB,然后利用“边角边”证明△MBG≌△NBH,再根据全等三角形对应边相等可得HN=MG,然后根据垂线段最短可得MG⊥CH时最短,再根据∠BCH=30°求解即可.
解:如图,取BC的中点G,连接MG,
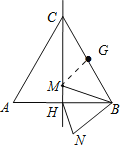
∵旋转角为60°,
∴∠MBH+∠HBN=60°,
又∵∠MBH+∠MBC=∠ABC=60°,
∴∠HBN=∠GBM,
∵CH是等边△ABC的对称轴,
∴HB=![]() AB,
AB,
∴HB=BG,
又∵MB旋转到BN,
∴BM=BN,
在△MBG和△NBH中,
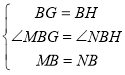 ,
,
∴△MBG≌△NBH(SAS),
∴MG=NH,
根据垂线段最短,当MG⊥CH时,MG最短,即HN最短,
此时∠BCH=![]() ×60°=30°,CG=
×60°=30°,CG=![]() AB=
AB=![]() ×12=6,
×12=6,
∴MG=![]() CG=
CG=![]() ×6=3,
×6=3,
∴HN=3;
故选:B.


科目:初中数学 来源: 题型:
【题目】材料阅读:
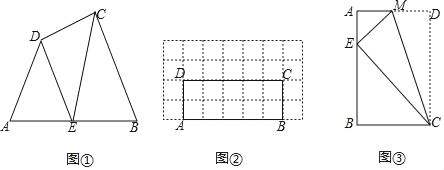
如图①,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点(无需写解答过程);
(3)如图③所示的矩形ABCD,将矩形ABCD沿CM折叠后,点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究点E的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BF平分∠ABC,交CD于点E,交AC于点F.若AB=10,BC=6,则CE的长为( )

A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某校有一块菱形空地ABCD,∠A=60°,AB=40m,现计划在内部修建一个四个顶点分别落在菱形四条边上的矩形鱼池EFGH,其余部分种花草,园林公司修建鱼池,草坪的造价为y(元)与修建面积s(m2)之间的函数关系如图2所示,设AE为x米.
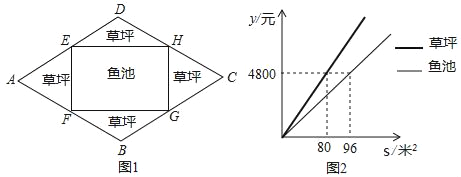
(1)填空:ED= m,EH= m,(用含x的代数式表示);
(提示:在直角三角形中,30°角所对的直角边等于斜边的一半)
(2)若矩形鱼池EFGH的面积是300![]() m2,求EF的长度;
m2,求EF的长度;
(3)EF的长度为多少时,修建的鱼池和草坪的总造价最低,最低造价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中![]() 、
、![]() 、
、![]() .
.
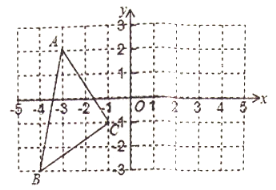
(1)在图中作出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ;
;
(2)写出![]() 、
、![]() 、
、![]() 的坐标,分别是
的坐标,分别是![]() (____,_____)、
(____,_____)、![]() (____,_____)、
(____,_____)、![]() (____,_____);
(____,_____);
(3)![]() 的面积是______________.
的面积是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.

(1)求证:①△BCG≌△DCE;②BH⊥DE.
(2)当点G运动到什么位置时,BH垂直平分DE?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
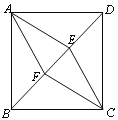
【题目】如图,在正方形ABCD中,点E、F在对角线BD上,且BF=DE.
⑴求证:四边形AECF是菱形.
⑵若AB=2,BF=1,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
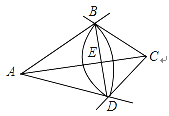
【题目】如图,在![]() 中,按如下步骤作图:
中,按如下步骤作图:
①以点A为圆心,AB长为半径画弧;
②以点C为圆心,CB长为半径画弧,两弧相交于点D;
③连接BD,与AC交于点E,连接AD、CD;
(1)求证:![]() ;
;
(2)当![]() 时,猜想四边形ABCD是什么四边形,并证明你的结论;
时,猜想四边形ABCD是什么四边形,并证明你的结论;
(3)当![]() ,
,![]() ,现将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长是多少?
,现将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com