
【题目】材料阅读:
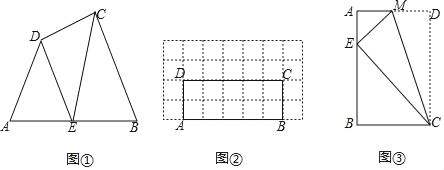
如图①,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点(无需写解答过程);
(3)如图③所示的矩形ABCD,将矩形ABCD沿CM折叠后,点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究点E的位置.
【答案】(1)点E是四边形ABCD的边AB上的相似点;(2)详见解析;(3)E为AB的中点.
【解析】
(1)要证明点E是四边形ABCD的AB边上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解;
(2)以CD为直径画弧,取该弧与AB的一个交点即为所求;
(3)由点E是矩形ABCD的AB边上的一个强相似点,得△AEM∽△BCE∽△ECM,根据相似三角形的对应角相等,可求得∠BCE=![]() ∠BCD=30°,利用含30°角的直角三角形性质可得BE与AB,边之间的数量关系,从而可求出E点的位置.
∠BCD=30°,利用含30°角的直角三角形性质可得BE与AB,边之间的数量关系,从而可求出E点的位置.
解:(1)点E是四边形ABCD的边AB上的相似点,理由是:
∵∠A=40°,
∴∠ADE+∠DEA=140°,
∵∠DEC=40°,
∴∠BEC+∠DEA=140°,
∴∠ADE=∠BEC,
∵∠A=∠B,
∴△ADE∽△BEC,
∴点E是四边形ABCD的边AB上的相似点;
(2)作图如下:
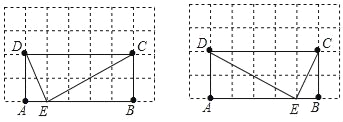
(3)若点E恰好是四边形ABCM的边AB上的一个强相似点,
则△AEM∽△BCE∽△ECM,
∴∠BCE=∠ECM=∠AEM,
由折叠得:∠ECM=∠DCM,CE=CD,
∴∠BCE=![]() ∠BCD=30°,
∠BCD=30°,
∴BE=![]() CE=
CE=![]() AB,
AB,
即E为AB的中点.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,六边形 ABCDEF 中,∠A+∠B+∠C=∠D+∠E+∠F,猜想可 得六边形 ABCDEF 中必有两条边是平行的.

(1)根据图形写出你的猜想: ∥ ;
(2)请证明你在(1)中写出的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
“ a 2 ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
x2 4x 5 x2 4x 4 1 x 22 1 ,
∵ x 22 ≥0,
∴ x 22 1 ≥1,
∴ x2 4x 5 ≥1.
试利用“配方法”解决下列问题:
(1)填空: x2 4x 5 ( x )2+ ;
(2)已知 x2 4x y2 2y 5 0 ,求 x y 的值;
(3)比较代数式 x2 1与2x 3 的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=1,BC=![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在社会主义新农村建设中,某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙工程先单独做10天,那么剩下的工程还需要两队合做20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)求两队合作完成这项工程所需的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
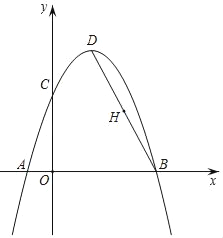
【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
(1)求抛物线的解析式及顶点D的坐标;
(2)在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为 .
(注:抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣![]() ,顶点坐标为(﹣
,顶点坐标为(﹣![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为12的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是( )
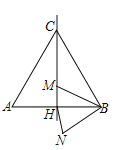
A.6B.3C.2D.1.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com