
����Ŀ����ͼ1��ijУ��һ�����οյ�ABCD����A=60�㣬AB=40m���ּƻ����ڲ���һ���ĸ�����ֱ����������������ϵľ������EFGH�����ಿ���ֻ��ݣ��ֹ�˾����أ���ƺ�����Ϊy��Ԫ���������s��m2��֮��ĺ�����ϵ��ͼ2��ʾ����AEΪx�ף�
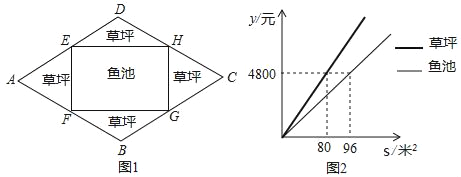
��1����գ�ED=�� ��m��EH=�� ��m�����ú�x�Ĵ���ʽ��ʾ����
����ʾ����ֱ���������У�30������Ե�ֱ�DZߵ���б�ߵ�һ�룩
��2�����������EFGH�������300![]() m2����EF�ij��ȣ�
m2����EF�ij��ȣ�
��3��EF�ij���Ϊ����ʱ��������غͲ�ƺ���������ͣ�������Ϊ����Ԫ��
���𰸡���1��![]() ��
��![]() �� ��2��10m��30m����3��x=20ʱ���������С����СֵΪ
�� ��2��10m��30m����3��x=20ʱ���������С����СֵΪ![]() Ԫ��
Ԫ��
��������
(1)ֱ��д���������.
(2)����DB���ж���AEFΪ�ȱ������Σ��Ӷ�EF=x������(1)��EH�ij������ݾ��������ʽ�г����̣����x����.
(3)����ͼ2�ó���ƺ����صļۣ��ֱ������ƺ����ص����(�ú�x��ʽ�ӱ�ʾ)���Ӷ��õ�һ���ܼ�Ϊһ������x���κ���������д�ɶ���ʽ����ɵó���������ֵ.
��1��![]() ��
��![]() ��
��
��2������![]() ����EF��DB
����EF��DB
��![]()
�� ![]()
��![]()
��![]()
���![]() �ǵȱ�������
�ǵȱ�������
��![]()
�ɣ�1����֪![]()
��![]()
![]()
![]()
���![]() ��
��![]() ��������������⣬
��������������⣬
��![]() �ij���10
�ij���10![]() ��30
��30![]() ��
��
��3��������ò�ƺ����Ϊ��4800��80=60Ԫ/��2��
��ص���Ϊ��4800��96=50Ԫ/��2��
���ı���ABCD�����Σ���BAD=60�㣬AB=40m����BD=40��AC=![]() ��
��
������ABCD������ǣ�![]()
![]() ��
��
�߾���EFGH������ǣ�![]()
���ƺ������ǣ�![]()
�������![]()
![]()
![]()
��![]()
�൱![]() ʱ���������С����СֵΪ
ʱ���������С����СֵΪ![]() Ԫ
Ԫ
��EF�ij���Ϊ20mʱ��������غͲ�ƺ���������ͣ�������![]() Ԫ��
Ԫ��
�ʴ�Ϊ����1��![]() ��
��![]() �� ��2��10m��30m����3��x=20ʱ���������С����СֵΪ
�� ��2��10m��30m����3��x=20ʱ���������С����СֵΪ![]() Ԫ.
Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��F�ֱ��DZ�AD��CD�ϵĵ㣬AE=ED��DF=![]() DC������EF���ӳ���BC���ӳ����ڵ�G��
DC������EF���ӳ���BC���ӳ����ڵ�G��
��1����֤����ABE�ס�DEF��
��2���������εı߳�Ϊ4����BG�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
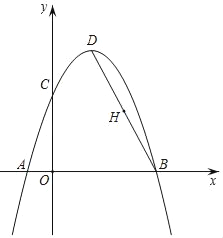
����Ŀ����ͼ��������y=��x2+bx+c����A����1��0����B��3��0�����㣬��y���ڵ�C����DΪ�����ߵĶ��㣬����BD����HΪBD���е㣮�����������⣺
��1���������ߵĽ���ʽ������D�����ꣻ
��2����y������һ��P��ʹPD+PH��ֵ��С����PD+PH����СֵΪ�� ����
��ע��������y=ax2+bx+c��a��0���ĶԳ�����ֱ��x=��![]() ����������Ϊ����
��������������![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() �ֱ��ڵȱ�������
�ֱ��ڵȱ�������![]() �ı�
�ı�![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() �����½��ۣ���
�����½��ۣ���![]() ����
����![]() ����
����![]() �������
�������![]() �����2������
�����2������![]() ��һ����ȷ���У� ������
��һ����ȷ���У� ������
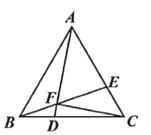
A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ��ֱ������ϵ�У���ABC���������������ֱ�ΪA��2��2����B��1����1����C��3��0����
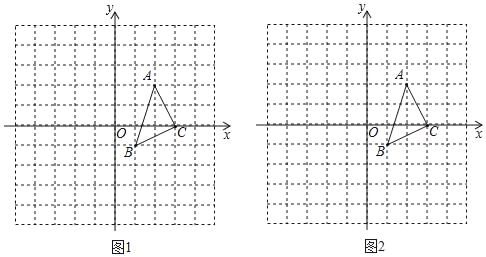
��1����ͼ1�У������Ե�OΪλ�����ģ��Ŵ���ABC��ԭ����2������A1B1C1��
��2����P��a��b����AB����һ�㣬ƽ����ABC֮��P�Ķ�Ӧ��P'�������ǣ�a+3��b��2������ͼ2�л���ƽ�ƺ����A2B2C2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���AB�Ĵ�ֱƽ���߽�AD�ڵ�E����CB���ӳ����ڵ�F������AF��BE��
��1����֤����AGE�ա�BGF��
��2�����ж��ı���AFBE����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ12�ĵȱ�������ABC�У�M�Ǹ�CH����ֱ���ϵ�һ�����㣬����MB�����߶�BM�Ƶ�B��ʱ����ת60���õ�BN������HN�����ڵ�M�˶������У��߶�HN���ȵ���Сֵ�ǣ� ��
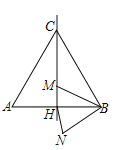
A.6B.3C.2D.1��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ��������ABOC�Ķ���O������ԭ������BO��x��ĸ�����������BOC=60�㣬����C������Ϊ��m��![]() ��������������
��������������![]() ��ͼ�������ζԽ���AO����D��������BD����BD��x��ʱ��k��ֵ����������
��ͼ�������ζԽ���AO����D��������BD����BD��x��ʱ��k��ֵ����������
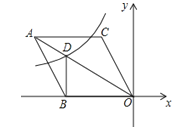
A. ![]() B. ��
B. ��![]() C.
C. ![]() D. ��
D. ��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��0��0����A��0��1����������![]() ���������㣬��
���������㣬��![]() �Խ���Ϊ����������
�Խ���Ϊ����������![]() �����������εĶԽ���
�����������εĶԽ���![]() ��������
��������![]() ���������˹��ɣ����
���������˹��ɣ����![]() �������ǣ� ��
�������ǣ� ��

A. ����8��0�� B. ��0��8��
C. ��0��8![]() �� D. ��0��16��
�� D. ��0��16��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com