
【题目】如图,点![]() ,
,![]() 分别在等边三角形
分别在等边三角形![]() 的边
的边![]() ,
,![]() 上,
上,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() ,连接
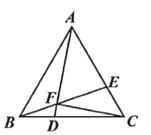
,连接![]() ,以下结论:①
,以下结论:①![]() ;②
;②![]() ;③
;③![]() 的面积是
的面积是![]() 面积的2倍;④
面积的2倍;④![]() ;一定正确的有( )个.
;一定正确的有( )个.
A.4B.3C.2D.1
 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:
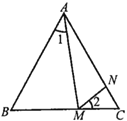
如图所示,在正![]() 中,
中,![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上,若
边上,若![]() ,则
,则![]() .小强是这样论证的:
.小强是这样论证的:
∵![]() 是正三角形,∴
是正三角形,∴![]() .∴
.∴![]() .
.
又因为![]() ,
,![]() ,∴
,∴![]() .∴
.∴![]() .
.
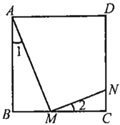
(1)类比应用:如图所示,将阅读理解中的正三角形换成正四边形![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的点,类似地:若
上的点,类似地:若![]() __________,则
__________,则![]() .请你用小强的证明方法论证.
.请你用小强的证明方法论证.
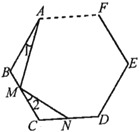
(2)拓展延伸:请你将上述命题推广到一般,如图所示,![]() …是正
…是正![]() 边形.
边形.
写出命题:______________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S1= ,Sn= (用含n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1,画出△A1B1C1.
(3)求(2)中C到C1经过的路径以及OB扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,BF平分∠ABC,交CD于点E,交AC于点F.若AB=10,BC=6,则CE的长为( )

A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某校有一块菱形空地ABCD,∠A=60°,AB=40m,现计划在内部修建一个四个顶点分别落在菱形四条边上的矩形鱼池EFGH,其余部分种花草,园林公司修建鱼池,草坪的造价为y(元)与修建面积s(m2)之间的函数关系如图2所示,设AE为x米.
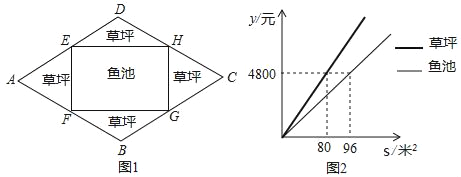
(1)填空:ED= m,EH= m,(用含x的代数式表示);
(提示:在直角三角形中,30°角所对的直角边等于斜边的一半)
(2)若矩形鱼池EFGH的面积是300![]() m2,求EF的长度;
m2,求EF的长度;
(3)EF的长度为多少时,修建的鱼池和草坪的总造价最低,最低造价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠B=50°,∠C=70°,AD是△ABC的角平分线,DE⊥AB于E点.
(1)求∠EDA的度数;
(2)AB=10,AC=8,DE=3,求S△ABC.

查看答案和解析>>
科目:初中数学 来源: 题型:
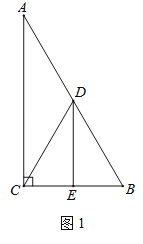
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;

(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com