
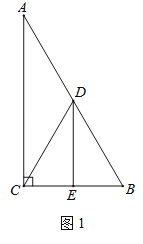
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;

(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.

【答案】解:(1)DE=![]() BC。
BC。
(2)根据旋转的性质得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,根据“SAS”可判断△DCP≌△DBF,则CP=BF,利用CP=BC﹣BP,DE=![]() BC可得到BF+BP=
BC可得到BF+BP=![]() DE;
DE;
(3)补全图形如图,DE、BF、BP三者之间的数量关系为BF﹣BP=![]() DE。
DE。
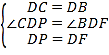
【解析】试题分析:(1)由∠ACB=90°,∠A=30°得到∠B=60°,根据直角三角形斜边上中线性质得到DB=DC,则可判断△DCB为等边三角形,由于DE⊥BC,DE=![]() BC;
BC;
(2)根据旋转的性质得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,则可根据“SAS”可判断△DCP≌△DBF,则CP=BF,利用CP=BC﹣BP,DE=![]() BC可得到BF+BP=
BC可得到BF+BP=![]() DE;
DE;
(3)与(2)的证明方法一样得到△DCP≌△DBF得到CP=BF,而CP=BC+BP,则BF﹣BP=BC,所以BF﹣BP=![]() DE.
DE.
解:(1)∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵点D是AB的中点,
∴DB=DC,
∴△DCB为等边三角形,
∵DE⊥BC,
∴DE=![]() BC;
BC;
故答案为DE=![]() BC.
BC.
(2)BF+BP=![]() DE.理由如下:
DE.理由如下:
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
而∠CDB=60°,
∴∠CDB﹣∠PDB=∠PDF﹣∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中
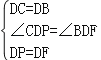 ,
,
∴△DCP≌△DBF(SAS),
∴CP=BF,
而CP=BC﹣BP,
∴BF+BP=BC,
∵DE=![]() BC,
BC,
∴BC=![]() DE,
DE,
∴BF+BP=![]() DE;
DE;
(3)如图,
与(2)一样可证明△DCP≌△DBF,
∴CP=BF,
而CP=BC+BP,
∴BF﹣BP=BC,
∴BF﹣BP=![]() DE.
DE.



科目:初中数学 来源: 题型:
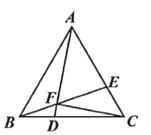
【题目】如图,点![]() ,
,![]() 分别在等边三角形
分别在等边三角形![]() 的边
的边![]() ,
,![]() 上,
上,![]() ,
,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,以下结论:①
,以下结论:①![]() ;②
;②![]() ;③
;③![]() 的面积是
的面积是![]() 面积的2倍;④
面积的2倍;④![]() ;一定正确的有( )个.
;一定正确的有( )个.
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
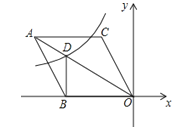
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A. ![]() B. -
B. -![]() C.
C. ![]() D. -
D. -![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
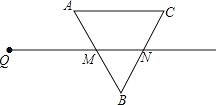
查看答案和解析>>
科目:初中数学 来源: 题型:
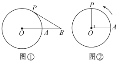
【题目】如图①②,A是半径为12cm的☉O上的定点,动点P从A出发,以2π(cm/s)的速度沿圆周逆时针运动,当点P回到A时立即停止运动.
(1)如图①,点B是OA延长线上一点,AB=OA,当点P运动时间为2s时,试证明直线BP是☉O的切线.
(2)如图②,当∠POA=90°时,求点P的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同完成一项工程,乙队先单独做1天后,再由两队合作2天就完成了全部工程.已知甲队单独完成工程所需的天数是乙队单独完成所需天数的![]() ,求甲、乙两队单独完成各需多少天?
,求甲、乙两队单独完成各需多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O(0,0),A(0,1)是正方形![]() 的两个顶点,以
的两个顶点,以![]() 对角线为边作正方形
对角线为边作正方形![]() ,再以正方形的对角线
,再以正方形的对角线![]() 作正方形
作正方形![]() ,…,依此规律,则点
,…,依此规律,则点![]() 的坐标是( )
的坐标是( )

A. (-8,0) B. (0,8)
C. (0,8![]() ) D. (0,16)
) D. (0,16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的⊙O经过点D.

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com