
【题目】某机动车出发前油箱内有42升油,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示.回答下列问题:
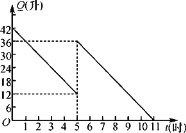
(1)机动车行驶几小时后,在途中加油站加油?
(2)求加油前油箱剩余油量Q与行驶时间t的函数关系,并求自变量t的取值范围;
(3)中途加油多少升?
(4)如果加油站距目的地还有320千米,车速为60千米/时,要到达目的地,油箱中的油是否够用?请说明理由.
【答案】(1)机动车行驶5小时后加油;(2)Q=42-6t(0≤t≤5);(3)中途加油24升;(4)油箱中的油够用,理由详见解析
【解析】
(1)观察函数图象,即可得出结论;
(2)根据每小时耗油量=总耗油量÷行驶时间,即可求出机动车每小时的耗油量,再根据加油前油箱剩余油量=42每小时耗油量×行驶时间,即可得出结论;
(3)根据函数图象中t=5时,Q值的变化,即可求出中途加油量;
(4)根据可行驶时间=油箱剩余油量÷每小时耗油量,即可求出续航时间,由路程=速度×时间,即可求出续航路程,将其与320比较后即可得出结论.
解:(1)观察函数图象可知:机动车行驶5小时后加油.
(2)机动车每小时的耗油量为(42-12)÷5=6(升),
∴加油前油箱剩余油量Q与行驶时间t的函数关系为Q=42-6t(0≤t≤5)
(3)36-12=24(升).
∴中途加油24升.
(4)油箱中的油够用.
理由:
∵加油后油箱里的油可供行驶11-5=6(小时),
∴剩下的油可行驶6×60=360(千米).
∵360>320,
∴油箱中的油够用.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中![]() 、
、![]() 、
、![]() .
.
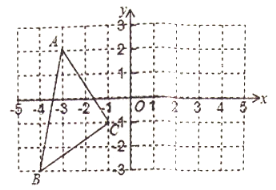
(1)在图中作出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ;
;
(2)写出![]() 、
、![]() 、
、![]() 的坐标,分别是
的坐标,分别是![]() (____,_____)、
(____,_____)、![]() (____,_____)、
(____,_____)、![]() (____,_____);
(____,_____);
(3)![]() 的面积是______________.
的面积是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
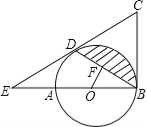
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
京通公交快速通道开通后,为响应市政府“绿色出行”的号召,家住通州新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米.他用乘公交车的方式平均每小时行驶的路程比他自用驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶多少千米?
.小王用自驾车方式上班平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
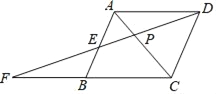
【题目】如图,在菱形ABCD中,P是对角线AC上的一点,连结DP并延长交AB于点E,交CB的延长线于点F.若DP=3,EF=![]() ,则PE的长是( )
,则PE的长是( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
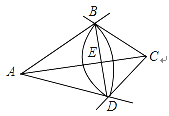
【题目】如图,在![]() 中,按如下步骤作图:
中,按如下步骤作图:
①以点A为圆心,AB长为半径画弧;
②以点C为圆心,CB长为半径画弧,两弧相交于点D;
③连接BD,与AC交于点E,连接AD、CD;
(1)求证:![]() ;
;
(2)当![]() 时,猜想四边形ABCD是什么四边形,并证明你的结论;
时,猜想四边形ABCD是什么四边形,并证明你的结论;
(3)当![]() ,
,![]() ,现将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长是多少?
,现将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个运算装置,当输入值为x时.其输出值为y,且y是x的二次函数.已知输入值为﹣2,0,1时,相应的输出值分别为5,﹣3,﹣4.
(1)求二次函数的关系式;
(2)如图,在所给的坐标系中画出这个二次函数的图象,并根据图象写出当输出值y为正数时,输入值x的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
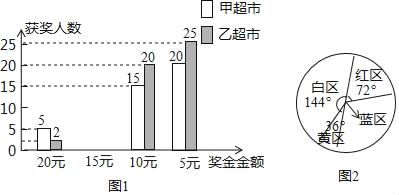
【题目】两家超市同时采取通过摇奖返现金搞促销活动,凡在超市购物满100元的顾客均可以参加摇奖一次.小明和小华对两家超市摇奖的50名顾客获奖情况进行了统计并制成了图表(如图)
奖金金额 获奖人数 | 20元 | 15元 | 10元 | 5元 |
商家甲超市 | 5 | 10 | 15 | 20 |
乙超市 | 2 | 3 | 20 | 25 |
(1)在甲超市摇奖的顾客获得奖金金额的中位数是 ,在乙超市摇奖的顾客获得奖金金额的众数是 ;
(2)请你补全统计图1;
(3)请你分别求出在甲、乙两超市参加摇奖的50名顾客平均获奖多少元?
(4)图2是甲超市的摇奖转盘,黄区20元、红区15元、蓝区10元、白区5元,如果你购物消费了100元后,参加一次摇奖,那么你获得奖金10元的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
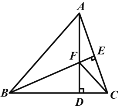
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=2,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com