练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

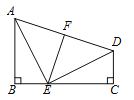
    【题目】如图：AB⊥BC，DC⊥BC，E在BC上，AB＝EC，BE＝CD，EF⊥AD于F.

    (1)求证：F是AD中点；

    (2)求∠AEF的度数.

    【答案】（1）证明见解析；（2）45°

    【解析】试题分析：（1）由题意，AB⊥BC，DC⊥BC，AB=EC，BE=CD，可证△ABE≌△ECD，可证AE=ED，且EF⊥AD，即可得证F是AD是中点．

    （2）由（1）可推出，△AED为等腰直角三角形，所以∠AEF=45°．

    试题解析：由题意，AB⊥BC，DC⊥BC，AB=EC，BE=CD，

    所以△ABE≌△ECD，

    所以AE=ED，

    又EF⊥AD，

    即可得证F是AD是中点；

    （2）由（1）得，∠AEB+∠CED=90°；

    所以∠AED=90°，

    所以△AED为等腰直角三角形，

    所以∠AEF=45°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图为4×4的正方形网格，图中的线段均为格点线段（线段的端点为格点），则∠1+∠2+∠3+∠4+∠5的度数为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算正确的是（ ）
    A.a2+a2=a4
    B.（﹣b2）3=﹣b6
    C.2x2x2=2x3
    D.（m﹣n）2=m2﹣n2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

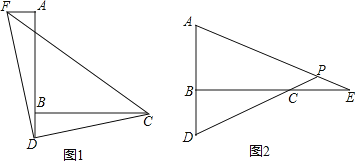
    【题目】（本小题满分11分）已知∠ABC=90°，D是直线AB上的点，AD=BC．

    （1）如图1，过点A作AF⊥AB，并截取AF=BD，连接DC、DF、CF，判断△CDF的形状并证明；

    （2）如图2，E是直线BC上一点，且CE=BD，直线AE、CD相交于点P，∠APD的度数是一个固定的值吗？若是，请求出它的度数；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

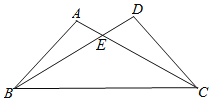
    【题目】（本小题满分8分）如图，已知∠A=∠D，有下列五个条件：①AE=DE，②BE=CE，③AB=DC，④∠ABC=∠DCB，⑤AC=BD，能证明△ABC与△DCB全等的条件有几个？并选择其中一个进行证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

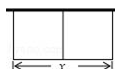
    【题目】如图，要建一个长方形养鸡场，鸡场的一边靠墙（墙足够长），如果用50m长的篱笆围成中间有一道篱笆墙的养鸡场，设它的长度为x（篱笆墙的厚度忽略不计）．

    （1）要使鸡场面积最大，鸡场的长度应为多少米？

    （2）如果中间有n（n是大于1的整数）道篱笆墙，要使鸡场面积最大，鸡场的长应为多少米？比较（1）（2）的结果，要使鸡场面积最大，鸡场长度与中间隔离墙的道数有怎样的关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】因式分解x2y﹣y的正确结果是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

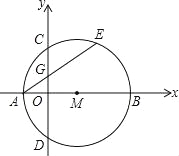
    【题目】如图，在平面直角坐标系xOy中，点m在x轴的正半轴上，⊙M交x轴于A、B两点，交y轴于C，D两点，且C为弧AE的中点，AE交y轴于G点，若点A的坐标为（﹣2，0），AE=8，

    （1）求证：AE=CD；

    （2）求点C坐标和⊙M直径AB的长；

    （3）求OG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果“盈利10%”记作+10%，那么“亏损6%”记作（ ）.
    A.-16%
    B.-6%
    C.+6%
    D.+4%

    查看答案和解析>>

    同步练习册答案