
【题目】(本小题满分11分)已知∠ABC=90°,D是直线AB上的点,AD=BC.
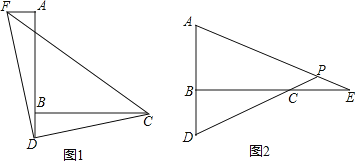
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
【答案】见解析
【解析】(1)△CDF是等腰直角三角形,(1分)
理由如下:
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,(2分)
在△FAD与△DBC中,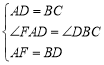 ,∴△FAD≌△DBC(SAS),(3分)
,∴△FAD≌△DBC(SAS),(3分)
∴FD=DC,∴△CDF是等腰三角形,(4分)
∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,∴△CDF是等腰直角三角形.(5分)
(2)作AF⊥AB于A,使AF=BD,连接DF,CF,如图,
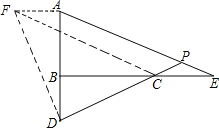
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,
在△FAD与△DBC中,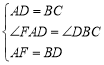 ,
,
∴△FAD≌△DBC(SAS),∴FD=DC,∴△CDF是等腰三角形,(6分)
∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形,(7分)
∴∠FCD=45°,(8分)
∵AF∥CE,且AF=CE,∴四边形AFCE是平行四边形,(10分)
∴AE∥CF,∴∠APD=∠FCD=45°.(11分)


科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题:
定义:线段AD把等腰三角形ABC分成△ABD与△ACD(如图1),如果△ABD与△ACD均为等腰三角形,那么线段AD叫做△ABC的完美分割线.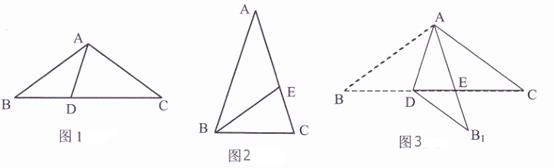
(1)如图1,已知△ABC中,AB=AC,∠BAC=108°,AD为△ABC的完美分割线,且BD<CD,则∠B= , ∠ADC=.
(2)如图2,已知△ABC中,AB=AC,∠A=36°,BE为△ABC的角平分线,求证:BE为△ABC完美分割线.
(3)如图3,已知△ABC是一等腰三角形纸片,AB=AC,AD是它的一条完美分割线,将△ABD沿直线AD折叠后,点B落在点B1处,AB1交CD于点E,求证:DB1=EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用量角器度量几个角的度数,下列结论中正确的是( )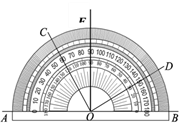
A.∠BOC=60°
B.∠COA是∠EOD 的余角
C.∠AOC=∠BOD
D.∠AOD与∠COE互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)已知n正整数,且 ![]() ,求
,求 ![]() 的值;
的值;
(2)如图,AB、CD交于点O,∠AOE=90°,若∠AOC︰∠COE=5︰4,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A>∠B.
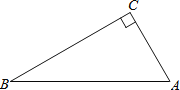
(1)用直尺和圆规作AB的垂直平分线,交AB与D,交BC于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若CE=DE,求∠A,∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com