
【题目】如图:已知A(0,-2),B(-2,1),C(3,2)
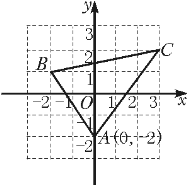
(1)求线段AB、BC、AC的长;
(2)把A、B、C三点的横坐标、纵坐标都乘以2,得到A′、B′、C′的坐标,求A′B′、B′C′、A′C′的长;
(3)以上六条线段成比例吗?
(4)△ABC与△A′B′C′的形状相同吗?
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)= ![]() . 例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=
. 例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= ![]() .
.
(Ⅰ)如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.
求证:对任意一个完全平方数m,总有F(m)=1;
(Ⅱ)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数t为“吉祥数”,求所有“吉祥数”;
(Ⅲ)在(2)所得“吉祥数”中,求F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为[x].即当n为非负整数时,若n﹣ ![]() ≤x<n+
≤x<n+ ![]() ,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
(1)填空:
①若[x]=3,则x应满足的条件:________;
②若[3x+1]=3,则x应满足的条件:________;
(2)求满足[x]= ![]() x﹣1的所有非负实数x的值.
x﹣1的所有非负实数x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点O是边AC上一个动点,过点O作直线
中,点O是边AC上一个动点,过点O作直线![]() //BC,分别交
//BC,分别交![]() ,外角
,外角![]() 的平分线于点E、F.
的平分线于点E、F.

(1)猜想与证明,试猜想线段OE与OF的数量关系,并说明理由.
(2)连接AE,AF,问:当点O在边AC上运动时到什么位置时,四边形AECF是矩形?并说明理由.
(3)若AC边上存在一点O,使四边形AECF是正方形,猜想![]() 的形状并证明你的结论.
的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标.
![]() ;
; ![]() ;
; ![]() ;
;
(3)求出△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①(﹣2)101+(﹣2)100=﹣2100;②20172+2017一定可以被2018整除;③16.9×![]() +15.1×
+15.1×![]() 能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
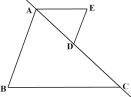
【题目】如图1,AB,BC被直线AC所截,点D是线段AC上的点,过点D作DE//AB,连接AE,∠B=∠E=70°.
(1)请说明AE//BC的理由.
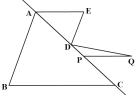
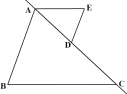
(2)将线段AE沿着直线AC平移得到线段PQ,连接DQ.
①如图2,当DE⊥DQ时,求∠Q的度数;
②在整个运动中,当∠Q=2∠EDQ时,则∠Q= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com