
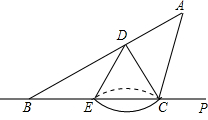
 如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥体底面圆的圆心,圆锥体的离为2
如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥体底面圆的圆心,圆锥体的离为2| 3 |
| 3 |
| 3 |
| 3 |

| 3 |
| DF |
| BD |
2
| ||
4
|
| 1 |
| 2 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…| 3 |
| 4100 |
| 3 |
| 4101 |
| 3 |
| 4102 |
| 3 |
| 4200 |
查看答案和解析>>
科目:初中数学 来源: 题型:
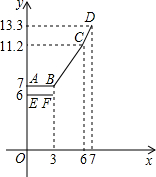 为缓解油价上涨给出租车行业带来的成本压力,某市自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
为缓解油价上涨给出租车行业带来的成本压力,某市自2007年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
| 行驶路程 | 收费标准 | |
| 调价前 | 调价后 | |
| 不超过3km的部分 | 起步价6元 | 起步价a元 |
| 超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
| 超出6km的部分 | 每公里c元 | |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
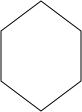 如图,表示一个正六菱柱形状的高大建筑物的俯视图.若该建筑物的高度为150米,底面正六边形的边长为50米.
如图,表示一个正六菱柱形状的高大建筑物的俯视图.若该建筑物的高度为150米,底面正六边形的边长为50米.查看答案和解析>>
科目:初中数学 来源: 题型:
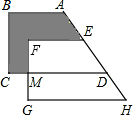 如图所示,把一梯形ABCD沿AD方向平移到角梯形EFGH,梯形ABCD的腰BC分别垂直于两底AB和CD,已知HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是
如图所示,把一梯形ABCD沿AD方向平移到角梯形EFGH,梯形ABCD的腰BC分别垂直于两底AB和CD,已知HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com