
 如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…
如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,记四边形A1ABB1的面积为S1;再分别取A1C、B1C的中点A2、B2,记四边形A2A1B1B2的面积为S2;再分别取A2C、B2C的中点A3、B3,依次取下去…| 3 |
| 4100 |
| 3 |
| 4101 |
| 3 |
| 4102 |
| 3 |
| 4200 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 42 |
| 3 |
| 42 |
| 3 |
| 4n |
| 3 |
| 4100 |
| 3 |
| 4 |
| 3 |
| 42 |
| 3 |
| 4100 |
| 3 |
| 4100 |
| 3 |
| 4101 |
| 3 |
| 4102 |
| 3 |
| 4200 |
| 1 |
| 499 |
| 1 |
| 4100 |
| 1 |
| 4100 |
| 1 |
| 4101 |
| 1 |
| 4200 |
| 1 |
| 499 |
| 1 |
| 4200 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
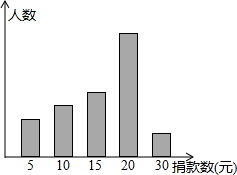 某中学对“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元得人数共39人.
某中学对“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元得人数共39人.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
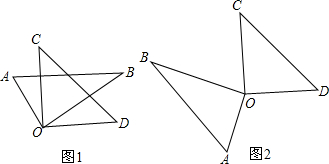 如图,将一副三角板的两个直角顶点O重合在一起,摆放成如图1、图2所示的形状.
如图,将一副三角板的两个直角顶点O重合在一起,摆放成如图1、图2所示的形状.查看答案和解析>>
科目:初中数学 来源: 题型:
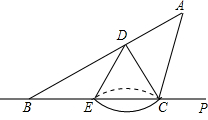 如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥体底面圆的圆心,圆锥体的离为2
如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥体底面圆的圆心,圆锥体的离为2| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com